Cho hình thang ABCD (hình vẽ). Biết diện tích các tam giác AED là \(2{\rm{c}}{{\rm{m}}^2}\) và BFC là \(3{\rm{c}}{{\rm{m}}^2}\). Tính diện tích tứ giác MENF
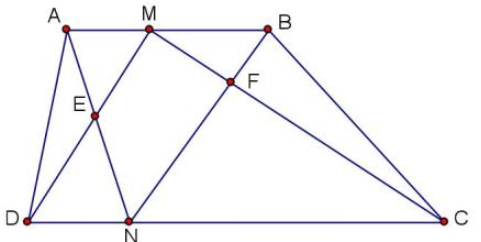
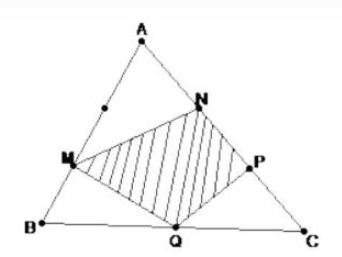
Cho hình thang ABCD (hình vẽ). Biết diện tích các tam giác AED là \(2{\rm{c}}{{\rm{m}}^2}\) và BFC là \(3{\rm{c}}{{\rm{m}}^2}\). Tính diện tích tứ giác MENF

Quảng cáo
Trả lời:
Ta có: \({S_{ADN}} = {S_{MDN}}\) (cùng đáy DN và có chiều cao bằng nhau)
\( \Rightarrow {S_{AED}} + {S_{EDN}} = {S_{MEN}} + {S_{EDN}} \Rightarrow {S_{ADE}} = {S_{MEN}} \Rightarrow {S_{MEN}} = 2{\rm{ c}}{{\rm{m}}^2}\)
Tương tự cũng có: \({S_{MCN}} = {S_{BCN}}\)
\( \Rightarrow {S_{MFN}} + {S_{FCN}} = {S_{BFC}} + {S_{FCN}} \Rightarrow {S_{MFN}} = {S_{BFC}} \Rightarrow {S_{MFN}} = 3{\rm{ c}}{{\rm{m}}^2}\)
Mà: \({S_{MENF}} = {S_{MEN}} + {S_{MFN}} \Rightarrow {S_{MEFN}} = 2 + 3 = 5{\rm{ c}}{{\rm{m}}^2}\)
Đáp Số: \(5{\rm{ c}}{{\rm{m}}^2}\)
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
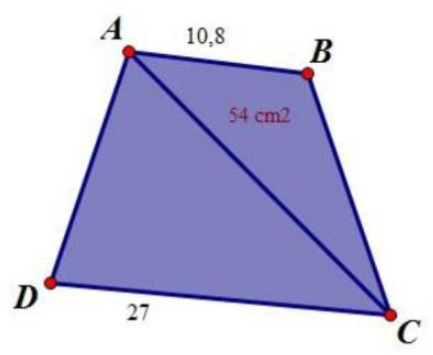
Chiều cao của tam giác ABC (hạ từ đỉnh C) cũng bằng chiều cao của hình thang và bằng chiều cao hạ từ A của tam giác ADC và nó bằng:
\(2 \times 54:10,8 = 10{\rm{ (cm)}}\)
Diện tích tam giác ADC là: \(27 \times 10:2 = 135{\rm{ (c}}{{\rm{m}}^2}{\rm{)}}\)
Đáp Số: \(135{\rm{ c}}{{\rm{m}}^2}\).
Lời giải
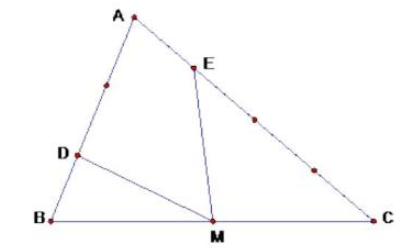
\({S_{MDB}} = \frac{1}{3} \times {S_{ABM}} = \frac{1}{3} \times \frac{1}{2} \times {S_{ABC}} = 3{\rm{ (c}}{{\rm{m}}^2}{\rm{)}}\)
\({S_{MCE}} = \frac{3}{4} \times {S_{ACM}} = \frac{3}{4} \times \frac{1}{2} \times {S_{ABC}} = 6,75{\rm{ (c}}{{\rm{m}}^2}{\rm{)}}\)
Do đó: \({S_{MDB}} + {S_{MCE}} = 3 + 6,75 = 9,75{\rm{ (c}}{{\rm{m}}^2}{\rm{)}}\)
Đáp Số: \(9,75{\rm{ c}}{{\rm{m}}^2}\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.