Một người đi từ A đến B bằng xe đạp trong 4 giờ với vận tốc 12 km/giờ, sau đó đi bằng xe máy trong 6 giờ thì đến B. Lúc về, người đó đi bằng xe máy trong 2 giờ rồi đi ô tô trong 3 giờ thì về đến A. Biết vận tốc xe máy bằng nửa vận tốc ô tô, tính độ dài quãng đưỡng AB?
Một người đi từ A đến B bằng xe đạp trong 4 giờ với vận tốc 12 km/giờ, sau đó đi bằng xe máy trong 6 giờ thì đến B. Lúc về, người đó đi bằng xe máy trong 2 giờ rồi đi ô tô trong 3 giờ thì về đến A. Biết vận tốc xe máy bằng nửa vận tốc ô tô, tính độ dài quãng đưỡng AB?
Câu hỏi trong đề: 13 bài tập Các dạng toán chuyển động khác có lời giải !!
Quảng cáo
Trả lời:
Do vận tốc xe máy bằng nửa vận tốc ô tô nên trên cùng một quãng đường thời gian ô tô đi chỉ bằng nửa thời gian xe máy đi.
Vậy ô tô đi quãng đường AB hết: \(2:2 + 3 = 4\) (giờ)
Vã quãng đường xe máy đi trong 6 giờ, ô tô đi trong: \(6:2 = 3\) (giờ)
Vậy quãng đường ô tô đi trong \(4 - 3 = 1\) giờ bằng quãng đường xe đạp đi trong 4 giờ là: \(4 \times 12 = 48\) km.
Vận tốc ô tô là: \(48:1 = 48\) (km/h)
Quãng đường AB là: \(48 \times 4 = 192\) (km)
Đáp Số : 192 km
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
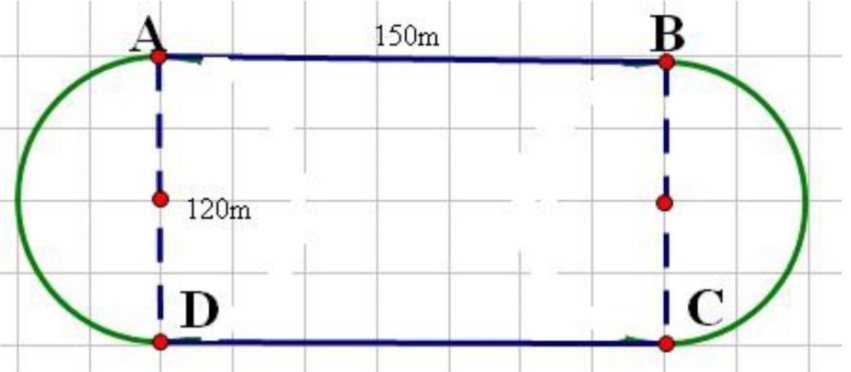
Mỗi nửa đường tròn dài: \(120 \times 3,14:2\) (mét)
Vậy hai nửa đường tròn dài: \(120 \times 3,14 = 376,8\) (m)
Cả đường chạy dài: \(376,8 + 150 \times 2 = 676,8\) (m)
Tổng vận tốc hai người chạy là: \(676,8:28,2 = 24\) (m/giây)
Hiệu vận tốc hai người là: \(676,8:338,4 = 2\) (m/giây)
Vận tốc của người chạy nhanh là: \((24 + 2):2 = 13\) (m/giây)
Vận tốc của người chạy chậm là: \(13 - 2 = 11\) (m/giây)
Đáp Số: 11 m/giây và 13 m/giây.
Lời giải
Thời gian bồ câu bay qua bay lại đúng bằng thời gian đơn vị thứ nhất hành quân để đuổi kịp đơn vị thứ hai. Thời gian đó là:
\(9:(6 - 4,5) = 6\) (giờ)
Quãng đường chim đã bay qua bay lại tất cả là:
\(28 \times 6 = 168\) (km)
Đáp Số: 168 km.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.