Câu hỏi:

13/08/2025 144

Ông An muốn xây một bể chứa nước dạng hình hộp chữ nhật, phần nắp trên ông để trống một ô có diện tích bằng $20\% $ diện tích của đáy bể. Biết đáy bể là một hình chữ nhật có chiều dài gấp đôi chiều rộng, biết bể có thể chứa tối đa $10{m^3}$ nước và giá tiền thuê nhân công là $500000$ đồng$/{m^2}$. Số tiền trả ít nhất cho nhân công mà ông phải trả gần nhất với số nào sau đây?

Trả lời: \[14\] triệu đồng.

Xem lời giải

Câu hỏi trong đề: (Trả lời ngắn) 32 bài tập GTLN, GTNN của hàm số (có lời giải) !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

$(Trả lời ngắn) Câu 30. Ông An muốn xây một bể chứa nước dạng hình hộp chữ nhật, phần nắp trên ông để trống một ô có diện tích bằng $20\% $ diện tích của đáy bể. Biết đáy bể là một hình chữ nhật có chiều dài gấp đôi chiều rộng, biết bể có thể chứa tối đa $10{m^3}$ nước và giá tiền thuê nhân công là $500000$ đồng$/{m^2}$. Số tiền trả ít nhất cho nhân công mà ông phải trả gần nhất với số nào sau đây? Trả lời: \[14\] triệu đồng. (ảnh 1)$

Gọi $x,\,y,\,z$ lần lượt là chiều rộng, chiều dài và chiều cao của cái bể ($x,\,y,\,z\, > \,0;\,\,y = 2x$). Đơn vị đo độ dài là mét $\left( m \right)$.

Theo đề bài ta có: $V = xyz = 2{x^2}z = 10$$ \Leftrightarrow z = \frac{5}{{{x^2}}}$ $\left( m \right)$.

Diện tích toàn phần cái bể:

$S = 2xz + 2xy + 2yz - \frac{1}{5}.xy$$ = 2x.\frac{5}{{{x^2}}} + 2x.2x + 2.2x.\frac{5}{{{x^2}}} - \frac{1}{5}.x.2x$$\left( {{m^2}} \right).$

$ \Leftrightarrow S = \frac{{30}}{x} + \frac{{16}}{5}{x^2} = \frac{{15}}{x} + \frac{{15}}{x} + \frac{{18}}{5}{x^2} \ge 3\sqrt[3]{{810}}\,\,\left( {{\mathop{\rm Cos}\nolimits} i} \right)$.

Dấu xảy ra $ \Leftrightarrow \frac{{15}}{x} = \frac{{18}}{5}{x^2}$ $ \Leftrightarrow x = \sqrt[3]{{\frac{{75}}{{18}}}} \Rightarrow S \approx 27,965$$\left( {{m^2}} \right).$

Vậy số tiền trả cho nhất công ít nhất là: $27,965 \times 500000 = 13.982.500$. Từ đó ta chọn đáp án

Hot: 1000+ Đề thi giữa kì 1 file word cấu trúc mới 2025 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Tìm giá trị lớn nhất, giá trị nhỏ nhất của các hàm số sau:
a) $y = x^{3} - 12 x + 1$ trên đoạn [-1;3]
b) $y = - x^{3} + 24 x^{2} - 180 x + 400$ trên đoạn [3;11]
c) $y = \frac{2 x + 1}{x - 2}$ trên đoạn $[3; 7]$
d) $y = \sin 2 x$ trên đoạn $[0; \frac{7 π}{12}]$

Trả lời:

a) $m a x_{[- 1; 3]} y = y (- 1) = 12$ và $m i n_{[- 1; 3]} y = y (2) = - 15$
b) $m a x_{[3; 11]} y = y (3) = 49$ và $m i n_{[3; 11]} y = y (6) = - 32$
c) $m a x_{[3; 7]} y = y (3) = 7$ và $m i n_{[3; 7]} y = y (7) = 3$
d) $m a x_{[0; \frac{7 π}{12}]} y = y (\frac{π}{4}) = 1$ và $m i n_{[0; \frac{7 π}{12}]} y = y (\frac{7 π}{12}) = - \frac{1}{2}$

Xem đáp án

Lời giải

a) Xét $y = x^{3} - 12 x + 1$ trên đoạn [-1;3]

$y' = 3 x^{2} - 12 = 0 \Leftrightarrow \{\begin{cases} x = 2 \\ x = - 2 (l o a i) \end{cases}$

Bảng biến thiên:

(Trả lời ngắn) Tìm giá trị lớn nhất, giá trị nhỏ nhất của các hàm số sau: a) y=x^3-12x+1 trên đoạn [-1;3] b) y=-x^3+24x^2-180x+400 trên đoạn [3;11] c) y=(2x+1)/(x-2) trên đoạn [3;7] d) y=sin⁡2x trên đoạn [0;7π/12] Trả lời: a) max_([-1;3]) y=y(-1)=12 và min_([-1;3]) y=y(2)=-15 b) max_([3;11]) y=y(3)=49 và min_([3;11]) y=y(6)=-32 c) max_([3;7]) y=y(3)=7 và min_([3;7]) y=y(7)=3 d) max_[0;7π/12] y=y(π/4)=1 và min_[0;7π/12] y=y(7π/12)=-1/2 (ảnh 1)

Từ bảng biến thiên, ta thấy $m a x_{[- 1; 3]} y = y (2) = - 15$ và
b) Xét $y = - x^{3}_24 x^{2} - 180 x + 400$ trên đoạn [3;11]

$y' = - 3 x^{2} + 48 x - 180 = 0 \Leftrightarrow \{\begin{cases} x = 10 \\ x = 6 \end{cases}$

Bảng biến thiên:

Từ bảng biến thiên, ta thấy $m a x_{[3; 11]} y = y (3) = 49$ và $m i n_{[3; 11]} y = y (6) = - 32$
c) Xét $y = \frac{2 x + 1}{x - 2}$ trên đoạn [3;7]

$y' = \frac{- 5}{{(x - 2)}^{2}} < 0 \forall x \in [3; 7]$

Bảng biến thiên:

Từ bảng biến thiên, ta thấy $m a x_{[3; 7]} y = y (3) = 7$ và $m i n_{[3; 7]} y = y (7) = 3$
d) Xét $y = \sin 2 x$ trên đoạn $[0; \frac{7 π}{12}]$

$y' = 2 \cos s 2 x = 0 \Leftrightarrow 2 x = \frac{π}{2} + k π \Leftrightarrow x = \frac{π}{4} + \frac{k π}{2} (k \in ℤ)$

Ta có: $x \in [0; \frac{7 π}{12}] \Rightarrow k = 0 \Rightarrow x = \frac{π}{4}$
Bảng biến thiên:

Từ bảng biến thiên, ta thấy $m a x_{[0; \frac{7 π}{12}]} y = (\frac{π}{4}) = 1$ và $m i n_{[0; \frac{7 π}{12}]} = y (\frac{7 π}{12}) = - \frac{1}{2}$

Câu 2

Người ta giăng lưới để nuôi riêng một loại cá trên một góc hồ. Biết rằng lưới được giăng theo một đường thẳng từ một vị trí trên bờ ngang đến một vị trí trên bờ dọc và phải đi qua một cái cọc đã cắm sẵn ở vị trí $A$. Hỏi diện tích nhỏ nhất có thể giăng là bao nhiêu, biết rằng khoảng cách từ cọc đến bờ ngang là $5\,m$ và khoảng cách từ cọc đến bờ dọc là $12\,m$.

$(Trả lời ngắn) Câu 31. Người ta giăng lưới để nuôi riêng một loại cá trên một góc hồ. Biết rằng lưới được giăng theo một đường thẳng từ một vị trí trên bờ ngang đến một vị trí trên bờ dọc và phải đi qua một cái cọc đã cắm sẵn ở vị trí $A$. Hỏi diện tích nhỏ nhất có thể giăng là bao nhiêu, biết rằng khoảng cách từ cọc đến bờ ngang là $5\,m$ và khoảng cách từ cọc đến bờ dọc là $12\,m$. Trả lời: $120{m^2}$. (ảnh 1)$
Trả lời: $120{m^2}$.

Xem đáp án

Lời giải

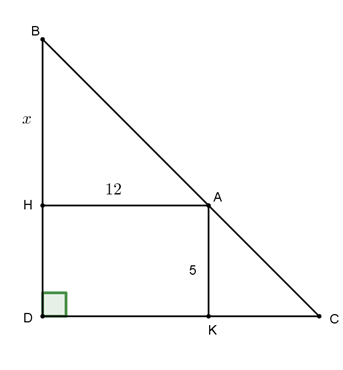
$(Trả lời ngắn) Câu 31. Người ta giăng lưới để nuôi riêng một loại cá trên một góc hồ. Biết rằng lưới được giăng theo một đường thẳng từ một vị trí trên bờ ngang đến một vị trí trên bờ dọc và phải đi qua một cái cọc đã cắm sẵn ở vị trí $A$. Hỏi diện tích nhỏ nhất có thể giăng là bao nhiêu, biết rằng khoảng cách từ cọc đến bờ ngang là $5\,m$ và khoảng cách từ cọc đến bờ dọc là $12\,m$. Trả lời: $120{m^2}$. (ảnh 2)$

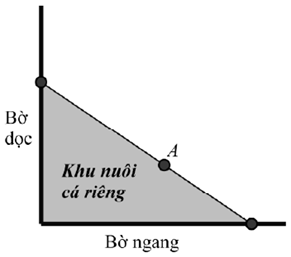
Gọi $H,\,K$ là hình chiếu của $A$ trên bờ dọc và bờ ngang. Đặt $BH = x\left( {x > 0} \right)$.

Khi đó, $\frac{{BH}}{{HD}} = \frac{{BA}}{{AC}} = \frac{{DK}}{{KC}} \Rightarrow KC = \frac{{HD.\,DK}}{{BH}} = \frac{{60}}{x}$.

Diện tích khu nuôi cá là:

$S = \frac{1}{2}BD.\,DC = \frac{1}{2}\left( {x + 5} \right)\left( {\frac{{60}}{x} + 12} \right) = 6x + \frac{{150}}{x} + 60 \ge 2\sqrt {6x.\frac{{150}}{x}} + 60$

$ \Rightarrow S \ge 120,\,S = 120\,\,khi\,\,x = 5$. Vậy diện tích nhỏ nhất có thể giăng là $120{m^2}$.

Câu 3