Cho hàm số \(y = \frac{{(m + 1){x^2} - 2mx + 6m}}{{x - 1}}\). Các mệnh đề sau đúng hay sai?
a) Với \(m = - 1\) thì hàm số đồng biến trên \(\left( {2; + \infty } \right)\)
b) Với \(m = 0\) thì hàm số nghịch biến trên \(\left( {1; + \infty } \right)\)
c) Hàm số đồng biến trên mỗi khoảng xác định khi và chỉ khi \(m\) thuộc \(\left[ {a;b} \right]\). Khi đó \(a + 5b = 0\)
d) Điều kiện cần và đủ để hàm số đồng biến trên \(\left( {4; + \infty } \right)\) là \(m \in \left[ { - 1; + \infty } \right)\).
Cho hàm số \(y = \frac{{(m + 1){x^2} - 2mx + 6m}}{{x - 1}}\). Các mệnh đề sau đúng hay sai?
a) Với \(m = - 1\) thì hàm số đồng biến trên \(\left( {2; + \infty } \right)\)
b) Với \(m = 0\) thì hàm số nghịch biến trên \(\left( {1; + \infty } \right)\)
c) Hàm số đồng biến trên mỗi khoảng xác định khi và chỉ khi \(m\) thuộc \(\left[ {a;b} \right]\). Khi đó \(a + 5b = 0\)
d) Điều kiện cần và đủ để hàm số đồng biến trên \(\left( {4; + \infty } \right)\) là \(m \in \left[ { - 1; + \infty } \right)\).
Quảng cáo
Trả lời:
+ TXĐ: \(D = \mathbb{R}\backslash \left\{ 1 \right\}\)
a. Với \(m = - 1:y = \frac{{2x - 6}}{{x - 1}} \Rightarrow y' = \frac{4}{{{{(x - 1)}^2}}},\,\forall x \in D\)
\( \Rightarrow \)Hàm số đồng biến trên mỗi khoảng xác định \(\left( { - \infty ;1} \right)\) và \(\left( {1; + \infty } \right)\)
\( \Rightarrow \)Hàm số đồng biến trên \(\left( {2; + \infty } \right)\)
\( \Rightarrow \)Mệnh đề a đúng
b. Với \(m = 0:y = \frac{{{x^2}}}{{x - 1}} \Rightarrow y' = 1 - \frac{1}{{{{(x - 1)}^2}}} = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = 2\end{array} \right.\)
Từ BBT của hàm số \(y = \frac{{{x^2}}}{{x - 1}} \Rightarrow \)Hàm số nghịch biến trên \(\left( {0;1} \right)\) và \(\left( {1;2} \right)\)
\( \Rightarrow \)Hàm số không nghịch biến trên \(\left( {1; + \infty } \right)\)
\( \Rightarrow \)Mệnh đề b sai
c. + TXĐ: \(D = \mathbb{R}\backslash \left\{ 1 \right\}\)
Xét hai trường hợp
TH1: Khi \(m = - 1,\) ta có hàm số \(y = \frac{{2x - 6}}{{x - 1}}\) và \(y' = \frac{4}{{{{(x - 1)}^2}}} > 0,\,\forall x \in D\)
Do đó hàm số đồng biến trên mỗi khoảng xác định
Vậy, \(m = - 1\) thỏa mãn yêu cầu bài toán
TH2: Khi \(m \ne - 1,\) ta có \(y' = \frac{{(m + 1){x^2} - 2(m + 1)x - 4m}}{{{{\left( {x - 1} \right)}^2}}}\)
Đặt \(g\left( x \right) = (m + 1){x^2} - 2\left( {m + 1} \right)x - 4m\) và ta có \(y'\) cùng dấu với \(g\left( x \right)\)
Hàm số đồng biến trên mỗi khoảng xác định\( \Leftrightarrow y' > 0,\,\forall x \in D \Leftrightarrow g\left( x \right) \ge 0,\,\forall x \in D\)
\( \Leftrightarrow \left\{ \begin{array}{l}\Delta ' = {(m + 1)^2} + 4m(m + 1) \le 0\\m + 1 > 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}(m + 1)(5m + 1) \le 0\\m > - 1\end{array} \right. \Leftrightarrow - 1 < m \le - \frac{1}{5}\)
Vậy tập hợp các giá trị của tham số \(m\)thỏa mãn yêu cầu của bài toán là \(\left[ { - 1; - \frac{1}{5}} \right]\)
d. Theo câu c \(m = - 1\) thỏa mãn đề bài
Với \(m \ne - 1\) Khi đó hàm số đồng biến trên khoảng \(\left( {4; + \infty } \right) \Leftrightarrow g\left( x \right) \ge 0,\,\forall x \in \left( {4; + \infty } \right)\)
\( \Leftrightarrow \frac{{2x - {x^2}}}{{{x^2} - 2x - 4}} \le m,\,\forall x \in \left( {4; + \infty } \right)\) Với mọi \(m\)dương hàm số luôn có 3 điểm cực trị.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 250+ Công thức giải nhanh môn Toán 12 (chương trình mới) ( 18.000₫ )
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
|
a) Đúng |
b) Đúng |
c) Sai |
d) Sai |
Tập xác định: \[D = \mathbb{R}\].
+Khi \(m = - 1\) ta có \[y = 2{x^3} + 6x + 2 \Rightarrow \]\[y' = 6{x^2} + 6 > 0\] nên hàm số luôn đồng biến trên \(\left( { - \infty ; + \infty } \right)\)
\( \Rightarrow \)a đúng
+Khi \(m = 1\) ta có \[y = 2{x^3} + 4{x^2} + 6x + 6 \Rightarrow \]\[y' = 6{x^2} + 8x + 6\]
Có \(\Delta ' = 16 - 36 = - 20 < 0\)\[ \Rightarrow y' = 6{x^2} + 8x + 6{\rm{ }}\forall x \in \mathbb{R}\] Hàm số không có cực trị khi \(m = 1\)\( \Rightarrow \)b đúng
Ta có: \[y' = 6{x^2} + 4\left( {m + 1} \right)x + 6\].
+ Hàm số \[y = 2{x^3} + 2\left( {m + 1} \right){x^2} + 6x + 4 + 2m\] đồng biến trên \[\mathbb{R}\] khi và chỉ khi
\[y' = 6{x^2} + 4\left( {m + 1} \right)x + 6 \ge 0{\rm{ }}\forall x \in \mathbb{R}\]
\[ \Leftrightarrow \Delta ' = 4{\left( {m + 1} \right)^2} - 36 \le 0 \Leftrightarrow {m^2} + 2m - 8 \le 0 \Leftrightarrow - 4 \le m \le 2.\]
Vậy \(m \in \left[ { - 4;2} \right]\)
Với \(m \in Z \Rightarrow m \in \left\{ { - 4; - 3; - 2; - 1;0;1;2} \right\} \Rightarrow c\) sai
+ có \[y'' = 12x + 4\left( {m + 1} \right)\]. Để hàm số đạt cực tiểu tại \(x = 2\) thì:
\(\left\{ {\begin{array}{*{20}{c}}{y'(2) = 0}\\{y''(2) > 0}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{38 + 8m = 0}\\{28 + 4m > 0}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{m = - \frac{{38}}{8}}\\{m > - 7}\end{array}} \right. \Leftrightarrow m = - \frac{{38}}{8}\)\( \Rightarrow \)d sai
Câu 2
Lời giải
Chọn D
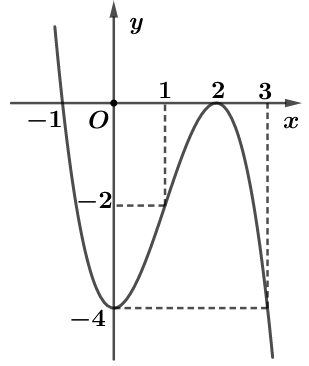
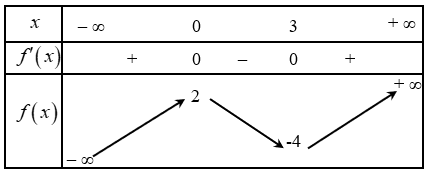
Từ đồ thị hàm số ta thấy hàm số \(y = f\left( x \right) + 2024\) đồng biến khoảng \(\left( {0\,;\,2} \right)\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.