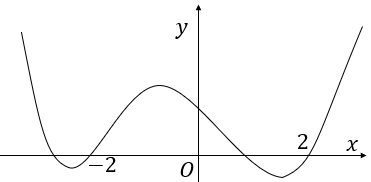
Cho hàm số \[y = f\left( x \right)\] có đạo hàm \(f'\left( x \right) = {x^2}\left( {x + 1} \right){\left( {x - 2} \right)^3}\), \(\forall x \in \mathbb{R}\). Hỏi hàm số đã cho có bao nhiêu điểm cực đại?
Quảng cáo
Trả lời:
Ta có: \(f'\left( x \right) = 0 \Leftrightarrow \left[ \begin{array}{l}{x^2} = 0\\x + 1 = 0\\{\left( {x - 2} \right)^3} = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = - 1\\x = 2\end{array} \right.\) .
Bảng biến thiên:
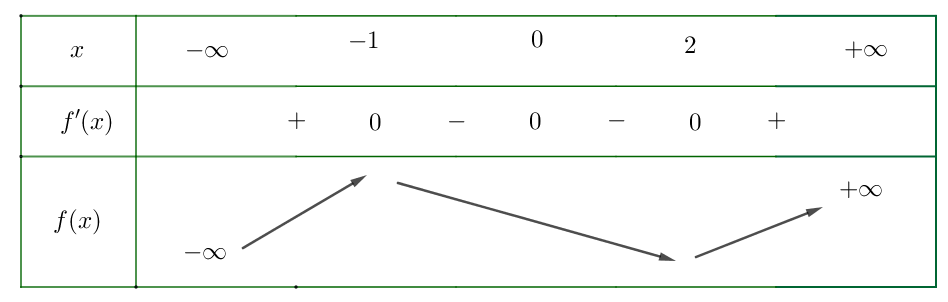
Dựa vào bảng biến thiên suy ra hàm số có \(1\) điểm cực đại.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 250+ Công thức giải nhanh môn Toán 12 (chương trình mới) ( 18.000₫ )
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
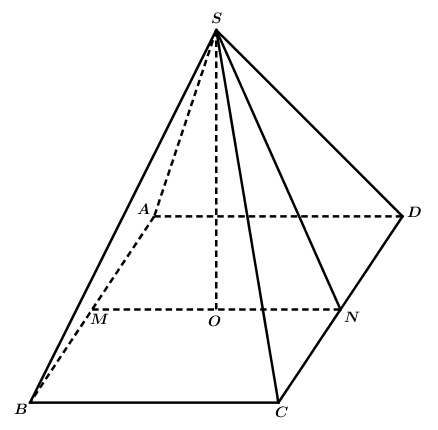
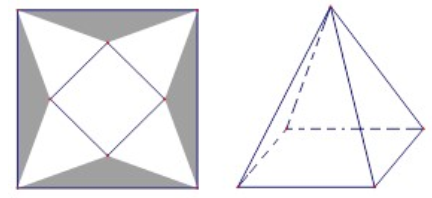
Gọi cạnh đáy hình vuông của tháp là \(x\left( m \right)\).
Độ dài đường chéo tấm bạt bằng \(20\sqrt 2 \,\left( m \right)\).
Gọi hình chóp tứ giác đều là \(S.ABCD\), Gọi\(M,N\) lần lượt là trung điểm \(AB,CD\).
Khi đó \(MN = x\left( m \right)\), \(SN = \frac{{20\sqrt 2 - x}}{2}\left( m \right)\) với \(0 < x < 10\sqrt 2 \).
Gọi \(O\) là tâm của hình vuông, ta có
\(SO = \sqrt {S{N^2} - O{N^2}} = \sqrt {{{\left( {\frac{{20\sqrt 2 - x}}{2}} \right)}^2} - {{\left( {\frac{x}{2}} \right)}^2}} = \frac{1}{2}\sqrt {800 - 40\sqrt 2 x} \).
Thể tích khối chóp \(V = \frac{1}{3}{S_{ABCD}}.SO = \frac{1}{6}{x^2}\sqrt {800 - 40\sqrt 2 x} \).
Ta có \(V' = \frac{{20x\left( {80 - 5\sqrt 2 x} \right)}}{{6\sqrt {800 - 40\sqrt 2 x} }}\)
\( \Rightarrow V' = 0 \Leftrightarrow x = 8\sqrt 2 \) với \(0 < x < 10\sqrt 2 \).
Xét bảng biến thiên:
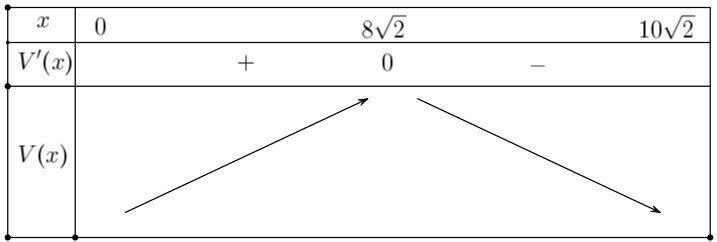
Vậy khi \(x = 8\sqrt 2 \) thì thể tích khối chóp lớn nhất \(V = \frac{{256\sqrt {10} }}{3}\left( {{m^3}} \right)\).
Diện tích phần bị cắt của tấm bạt:
\(S = {S_{hv}} - {S_{ABCD}} - 4.{S_{\Delta SAB}} = {20^2} - {\left( {8\sqrt 2 } \right)^2} - 4.\frac{1}{2}.\frac{{20\sqrt 2 - 8\sqrt 2 }}{2}.8\sqrt 2 = 80\left( {{m^2}} \right)\).
Lời giải
Tập xác định: \[\mathbb{R}\backslash \left\{ { - 1} \right\}\].
Ta có: \(y' = \frac{{{x^2} + 2x}}{{{{\left( {x + 1} \right)}^2}}}\), \(y' = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = - 2\end{array} \right.\).
Bảng xét dấu của \(y'\):
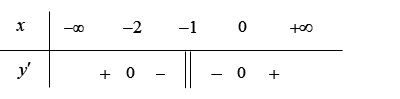
Vậy hàm số nghịch biến trên mỗi khoảng \(\left( { - 2\,;\, - 1} \right)\) và \(\left( { - 1\,;\,0} \right)\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
![Tìm tất cả các khoảng đồng biến của hàm số \[y = f\left( {2 - {x^2}} \right)\]. (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/09/13-1759133388.png)
![Hàm số \[y = f\left( x \right)\] đồng biến trên khoảng \(\left( { - \infty \,;\,0} \right)\), (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/09/screenshot-3626-1759133053.png)