Một mảnh đất hình thang vuông có đáy lớn gấp đôi đáy nhỏ, có diện tích là \(S = 24\,\left( {{m^2}} \right)\). Gọi \(x\,\left( m \right)\) là độ dài đáy nhỏ và \(P\left( x \right)\) là chu vi mảnh đất đó. Tìm số tiệm cận của \(P\left( x \right)\).
Một mảnh đất hình thang vuông có đáy lớn gấp đôi đáy nhỏ, có diện tích là \(S = 24\,\left( {{m^2}} \right)\). Gọi \(x\,\left( m \right)\) là độ dài đáy nhỏ và \(P\left( x \right)\) là chu vi mảnh đất đó. Tìm số tiệm cận của \(P\left( x \right)\).
Quảng cáo
Trả lời:
Gọi \(x\,\)là độ dài đáy nhỏ của hình thang \(\left( {x > 0} \right)\). Ta có :
Đáy lớn là \(2x\,\).
Chiều cao của hình thang là \(h = \frac{{2S}}{{x + 2x}}\, = \frac{{16}}{x}\).
Độ dài cạnh còn lại của hình thang là \[\sqrt {{x^2} + {{\left( {\frac{{16}}{x}} \right)}^2}} \, = \sqrt {{x^2} + \frac{{256}}{{{x^2}}}} \].
Khi đó \[P\left( x \right) = x + \frac{{16}}{x} + 2x + \sqrt {{x^2} + \frac{{256}}{{{x^2}}}} = 3x + \sqrt {{x^2} + \frac{{256}}{{{x^2}}}} + \frac{{16}}{x}\] (tập xác định \(D = \left( {0;\, + \infty } \right)\)).
Do \(\mathop {\lim }\limits_{x \to + \infty } P\left( x \right) = \mathop {\lim }\limits_{x \to + \infty } \left[ {3x + \sqrt {{x^2} + \frac{{256}}{{{x^2}}}} + \frac{{16}}{x}} \right] = \mathop {\lim }\limits_{x \to + \infty } x\left[ {3 + \sqrt {1 + \frac{{256}}{{{x^4}}}} + \frac{{16}}{{{x^2}}}} \right] = + \infty \) nên đồ thị hàm số không có tiệm cận ngang.
+ \(\mathop {\lim }\limits_{x \to {0^ + }} P\left( x \right) = \mathop {\lim }\limits_{x \to {0^ + }} \frac{1}{x}\left[ {3{x^2} + \sqrt {{x^4} + 256} + 16} \right] = + \infty \) nên đồ thị hàm số có một tiệm cận đứng là trục \(Oy\)
+\(\mathop {\lim }\limits_{x \to + \infty } \left( {P\left( x \right) - 4x} \right) = \mathop {\lim }\limits_{x \to + \infty } \left[ {\sqrt {{x^2} + \frac{{256}}{{{x^2}}}} - x + \frac{{16}}{x}} \right] = \mathop {\lim }\limits_{x \to + \infty } \left[ {\frac{{256}}{{{x^2}\sqrt {{x^2} + \frac{{256}}{{{x^2}}}} + x}} + \frac{{16}}{{{x^2}}}} \right] = 0\).
Khi đó đồ thị hàm số có 1 tiệm cận xiên \[y = 4x\].
Vậy đồ thị hàm số có 2 tiệm cận.
Hot: Danh sách các trường đã công bố điểm chuẩn Đại học 2025 (mới nhất) (2025). Xem ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
Lời giải
Ta có \(y = \frac{{{x^2} + 4x + 16}}{x} = x + 4 + \frac{{16}}{x}\).
\[\mathop {\lim }\limits_{x \to + \infty } \left[ {y - \left( {x + 4} \right)} \right] = \mathop {\lim }\limits_{x \to + \infty } \left( {\frac{{16}}{x}} \right) = 0,\,\,\mathop {\lim }\limits_{x \to - \infty } \left[ {y - \left( {x + 4} \right)} \right] = \mathop {\lim }\limits_{x \to - \infty } \left( {\frac{{16}}{x}} \right) = 0\]
Đồ thị hàm số có đường tiệm cận xiên: \(y = x + 4\).
Tọa độ giao điểm của đường tiệm cận xiên với hai trục tọa độ là : \(A\left( {0;\,4} \right),\,B\left( { - 4;\,0} \right)\).
Diện tích tam giác \(OAB\)là \(S = \frac{1}{2}.OA.OB = \frac{1}{2}4.4 = 8\).
Lời giải
Đáp án: \( - 9\).
Điều kiện: \(\left\{ \begin{array}{l}x \le 1\\{x^2} + 4x + m \ne 0\end{array} \right.\).
Ta có: 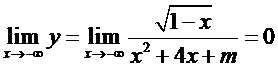 là tiệm cận ngang của đồ thị hàm số.
là tiệm cận ngang của đồ thị hàm số.
Đồ thị hàm số có \(3\) đường tiệm cận \( \Leftrightarrow \) Đồ thị hàm số có \(2\) đường tiệm cận đứng \( \Leftrightarrow \) Phương trình \({x^2} + 4x + m = 0\) có 2 nghiệm phân biệt thuộc \(\left( { - \infty ;1} \right]\).
Ta có: \({x^2} + 4x + m = 0\)\( \Leftrightarrow {x^2} + 4x = - m\).
Bảng biến thiên của hàm số \(y = g\left( x \right) = {x^2} + 4x\):
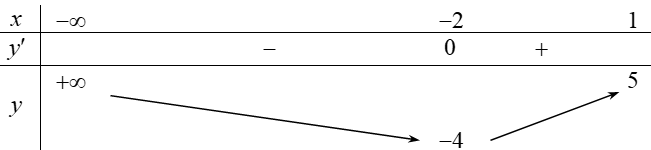
Phương trình \({x^2} + 4x + m = 0\) có 2 nghiệm phân biệt thuộc \(\left( { - \infty ;1} \right]\) ![]() \( \Leftrightarrow - 5 \le m < 4\).
\( \Leftrightarrow - 5 \le m < 4\).
\( \Rightarrow \)\(S = \left\{ { - 5\,;\, - 4\,;\, - 3\,;\, - 2\,;\, - 1\,;\,0\,;\,1\,;\,2\,;\,3\,} \right\}\).
Vậy tổng giá trị các phần tử của tập \(S\) bằng \( - 9\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
![Có bao nhiêu giá trị nguyên của tham số \(m\) thuộc \(\left[ {0\,;\,10} \right]\) để đồ thị hàm số \(y = \frac{{f\left( x \right)}}{{f\left( x \right) - m + 2}}\) có đúng 4 đường tiệm cận? (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/09/14-1759193871.png)
![Có bao nhiêu giá trị nguyên của tham số \[m\] để đồ thị hàm số \[g\left( x \right) = \frac{{{x^4} - {x^2} + 2020}}{{{f^2}\left( x \right) - 2\left( {m + 1} \right).f\left( x \right) + 5\left( {2m - 3} \right)}}\] có đúng \[6\] đường tiệm cận. (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/09/15-1759193910.png)