khoahoc.vietjack.com
Giảm 50% Kích hoạt VIP
khoahoc.vietjack.com
Kích hoạt VIP Đăng nhập
Tạo VIP
  2. Lớp 12
  3. Toán

Câu hỏi:

30/09/2025 10,274 Lưu

Trong một trò chơi, mỗi đội chơi được phát một tấm bìa hình chữ nhật kích thước 21 cm, 29,5 cm. Nhiệm vụ của mỗi đội là cắt ở bốn góc của tấm bìa này bốn hình vuông bằng nhau, rồi gập tấm bìa lại và dán keo để được một cái hộp không nắp có dạng hình hộp chữ nhật như hình vẽ. 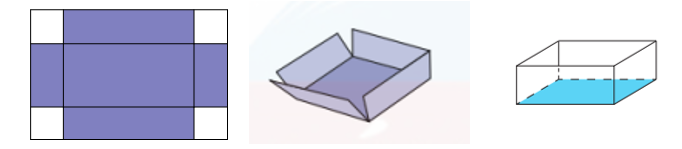Trong một trò chơi, mỗi đội chơi được phát một tấm bìa hình chữ nhật kích thước 21 cm, 29,5 cm. (ảnh 1)
Đội nào thiết kế được chiếc hộp có thể tích lớn nhất sẽ dành chiến thắng. Hãy xác định cạnh của hình vuông bị cắt để thu được hộp có thể tích lớn nhất. (Coi mép dán không đáng kể, kết quả làm tròn đến hàng phần trăm).

Xem lời giải

Câu hỏi trong đề: Đề kiểm tra Bài tập cuối chương 1 lớp 12 (có lời giải) !!

Flashcard Bắt Đầu Thi Giao bài

Quảng cáo

Trả lời:

verified Giải bởi Vietjack

Đáp số: \(4,03\;\;cm\).

Gọi cạnh của hình vuông bị cắt ở bốn góc là: \(x\).

Điều kiện: \(0 < 2x < 21 \Leftrightarrow 0 < x < 10,5\), đơn vị \(cm\).

Ta có kích thước của khối hộp chữ nhật là: \(x,{\kern 1pt} {\rm{ }}21 - 2x;\;29,{\rm{ }}5 - 2x\).

Thể tích của khối hộp là: \(V = \left( {21 - 2x} \right).\left( {29,5 - 2x} \right).x = 619,5x - 101{x^2} + 4{x^3} = f\left( x \right)\).

Thể tích khối hộp lớn nhất khi hàm số \(f\left( x \right)\) đạt giá trị lớn nhất.

\(f'\left( x \right) = 12{x^2} - 202x + 619,5 = 0 \Leftrightarrow \left[ \begin{array}{l}{x_2} \approx 12,80\\{x_1} \approx 4,03\end{array} \right.\).

 Ta có bảng biến thiên:

Trong một trò chơi, mỗi đội chơi được phát một tấm bìa hình chữ nhật kích thước 21 cm, 29,5 cm. (ảnh 2)

 Suy ra \[\mathop {\max }\limits_{\left( {0;10,5} \right)} f\left( x \right) = f\left( {{x_1}} \right)\].

Vậy cạnh của hình vuông xấp xỉ \(4,03\;cm\).

Đang tải chế độ Học...

Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay

ĐẶC QUYỀN VIP

Đăng ký VIP để học và luyện thi không giới hạn

Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.

  • Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
  • Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
  • Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
  • Tải xuống đề thi [DOCX] với đầy đủ đáp án
  • Xem bài giảng đính kèm củng cố thêm kiến thức
  • Bao gồm tất cả các bậc từ Tiểu học đến Đại học
  • Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
  • Đăng ký ngay
Avatar

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Phần 3: Câu trả lời ngắn

Sau khi phát hiện một dịch bệnh, các chuyên gia y tế ước tính số người nhiễm bệnh kể từ ngày phát hiện bệnh nhân đầu tiên đến ngày thứ \(t\) là \[f\left( t \right) = - {t^3} + 45{t^2} + 600t\], \[t \in \mathbb{N},{\rm{ }}t \le 30\]. Nếu coi \(f\left( t \right)\) là hàm số xác định trên đoạn \(\left[ {0;30} \right]\) thì \(f'\left( t \right)\) được xem là tốc độ truyền bệnh (người/ngày) tại thời điểm \(t\). Trong 30 ngày đầu tiên, có bao nhiêu ngày mà tốc độ truyền bệnh lớn hơn 1200?

Lời giải

Đáp số: \(9\).

Ta có \[f\left( t \right) =  - {t^3} + 45{t^2} + 600t \Rightarrow f'\left( t \right) =  - 3{t^2} + 90t + 600\].

Tốc độ truyền bệnh lớn hơn 1200 nên \[f'\left( t \right) > 1200 \Leftrightarrow  - 3{t^2} + 90t + 600 > 1200 \Leftrightarrow  - 3{t^2} + 90t - 600 > 0 \Leftrightarrow 10 < t < 20\].

Vậy có 9 ngày tốc độ truyền bệnh lớn hơn 1200.

Câu 2

Cho hàm số \[y = \frac{{a{x^2} + bx + 1}}{{cx + 2}}\] có đồ thị như hình vẽ bên dưới. Tính giá trị biểu thức: \(T = 2a + 3b - c\).

Cho hàm số \[y = \frac{{a{x^2} + bx + 1}}{{cx + 2}}\] có đồ thị như hình vẽ bên dưới. Tính giá trị biểu thức: \(T = 2a + 3b - c\). A. 9. B. 10. C. 8. D. 11. (ảnh 1)
A. 9.                           
B. 10.                       
C. 8.                               
D. 11.

Lời giải

Lời giải

Đồ thị có tiệm cận đứng \(x =  - 2\).

Suy ra \( - \frac{2}{c} =  - 2 \Leftrightarrow c = 1\).

Đồ thị có tiệm cận xiên đi qua hai điểm: \(\left( {0;1} \right)\) và \(\left( { - 1;0} \right)\) nên có phương trình: \(\frac{x}{{ - 1}} + \frac{y}{1} = 1 \Leftrightarrow y = x + 1\).

Khi đó ta có:

\[\mathop {\lim }\limits_{x \to  + \infty } \frac{{a{x^2} + bx + 1}}{{x\left( {x + 2} \right)}} = 1 \Leftrightarrow a = 1\]; \[\mathop {\lim }\limits_{x \to  + \infty } \left( {\frac{{{x^2} + bx + 1}}{{x + 2}} - x} \right) = \mathop {\lim }\limits_{x \to  + \infty } \frac{{\left( {b - 2} \right)x + 1}}{{x + 2}} = b - 2 = 1 \Leftrightarrow b = 3\].

Vậy: \(T = 2a + 3b - c = 2 + 9 - 1 = 10\). Chọn đáp án B.

Câu 3

Cho hàm số \[y = \frac{{ax + b}}{{cx - 1}}\] có đồ thị như hình vẽ bên dưới. Trong các hệ số \(a\), \(b\), \(c\) có bao nhiêu số dương?

Cho hàm số \[y = \frac{{ax + b}}{{cx - 1}}\] có đồ thị như hình vẽ bên dưới. Trong các hệ số \(a\), \(b\), \(c\) có bao nhiêu số dương? A. 0. B. 2. C. 1. D. 3. (ảnh 1)
A. 0.                           
B. 2.                         
C. 1.                               
D. 3.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 4

Biết tích các giá trị của tham số \(m\) để đồ thị của hàm số \(y = \frac{{2x - 4}}{{{x^2} + 2\left( {m - 2} \right)x + {m^2} + 1}}\) có đúng 2 đường tiệm cận là \(\frac{a}{b}\), \(\frac{a}{b}\) là phân số tối giản. Tính \(P = {a^2} + {b^2}\).

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 5

Tổng số đường tiệm cận của đồ thị hàm số \(y = \frac{{\sqrt x + 1}}{{3x - 9\sqrt x + 6}}\) là
A. 3.                           
B. 4.                         
C. 2.                               
D. 1.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 6

Phần 2: Trắc nghiệm đúng sai

Cho hàm số \(y = f\left( x \right)\) có đạo hàm trên \(\mathbb{R}\)và hàm số \(y = f'\left( x \right)\)là hàm số bậc ba có đồ thị là đường cong trong hình vẽ.

Xét tính đúng hoặc sai của các mệnh đề sau: a) [Mức độ 1] Hàm số \(y = f\left( x \right)\) đồng biến trên khoảng \(\left( { - \infty ; - 2} \right)\). (ảnh 1)

Xét tính đúng hoặc sai của các mệnh đề sau:

a) [Mức độ 1] Hàm số \(y = f\left( x \right)\) đồng biến trên khoảng \(\left( { - \infty ; - 2} \right)\).

b) [Mức độ 1] Hàm số \(y = f\left( x \right)\) có hai điểm cực trị.

c) [Mức độ 2] \(f'\left( 2 \right) = 4\).

d) [Mức độ 3] Hàm số \(g\left( x \right) = f\left( x \right) - \frac{1}{2}{x^2} + x + 2024\) đồng biến trên khoảng \(\left( { - \frac{5}{2}; - \frac{3}{2}} \right)\).

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Xem thêm các câu hỏi khác »

Đăng ký

Bằng cách đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của VietJack.

Bạn đã có tài khoản?

Khóa học 1 - 12
THPT
THCS
Phòng luyện đề
ĐGNL - ĐGTD
Tốt nghiệp THPT
Ôn vào 10
Ôn vào 6
Tài liệu
THPT
THCS
Tin Tuyển Sinh
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
Giấy chứng nhận ĐKKD số: 0108307822 do Sở KH & ĐT TP Hà Nội cấp lần đầu ngày 04/06/2018
© 2017 Vietjack87. All Rights Reserved.
zalo Nhắn tin Zalo Hỏi bài tập