Quảng cáo
Trả lời:
Giải bởi Vietjack
Điều kiện xác định: \(x \ge \frac{2}{3}\)
\(\sqrt x + \sqrt {3x - 2} = {x^2} + 1\)
\( \Leftrightarrow 2\sqrt x + 2\sqrt {3x - 2} = 2{x^2} + 2\)
\( \Leftrightarrow 2{x^2} + 2 - 2\sqrt x - 2\sqrt {3x - 2} = 0\)
\( \Leftrightarrow 2\left( {{x^2} - 2x + 1} \right) + \left( {x - 2\sqrt x + 1} \right) + \left( {3x - 2 - 2\sqrt {3x - 2} + 1} \right) = 0\)
\( \Leftrightarrow 2{\left( {x - 1} \right)^2} + {\left( {\sqrt x - 1} \right)^2} + {\left( {\sqrt {3x - 2} - 1} \right)^2} = 0\)
Ta có: \(\left\{ \begin{array}{l}2{\left( {x - 1} \right)^2} \ge 0\\{\left( {\sqrt x - 1} \right)^2} \ge 0\\{\left( {\sqrt {3x - 2} - 1} \right)^2} \ge 0\end{array} \right.,\forall x \ge \frac{2}{3}\)
Do đó \(2{\left( {x - 1} \right)^2} + {\left( {\sqrt x - 1} \right)^2} + {\left( {\sqrt {3x - 2} - 1} \right)^2} \ge 0\) nên để dấu bằng xảy ra thì \[\left\{ \begin{array}{l}2{\left( {x - 1} \right)^2} = 0\\{\left( {\sqrt x - 1} \right)^2} = 0\\{\left( {\sqrt {3x - 2} - 1} \right)^2} = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 1\\\sqrt x = 1\\\sqrt {3x - 2} = 1\end{array} \right.\]
\[ \Leftrightarrow x = 1\](thỏa mãn ĐKXĐ)
Kết luận: phương trình có một nghiệm duy nhất \(x = 1\).Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
|
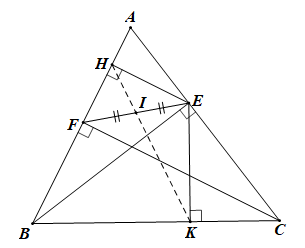
Chứng minh tứ giác \[BHEK\] nội tiếp. |
|
Ta có \(H,K\) là chân đường vuông góc từ \(E\) xuống \(AB\) \(BC\) nên \(\widehat {BHE} = 90^\circ \) và \(\widehat {BKE} = 90^\circ \) Suy ra \(\widehat {BHE} + \widehat {BKE} = 180^\circ \) Mà hai góc này ở vị trí đối nhau trong tứ giác \(BHEK\). Vậy tứ giác \(BHEK\) là tứ giác nội tiếp. |
|
Chứng minh \[BH.BA = BK.BC\] |
|
Áp dụng hệ thức lượng cho \(\Delta AEB\) vuông tại \(E\), đường cao \(EH\) có: \(BH.BA = B{E^2}\). Chứng minh tương tự ta có: \(BK.BC = B{E^2}\). Vậy \(BH.BA = BK.BC\). |
|
Chứng minh \[H,I,K\] thẳng hàng. |
|
Vì \(CF \bot AB\) tại \(F\) nên \(\widehat {BFC} = 90^\circ \) Vì \(BE \bot AC\) tại \(E\) nên \(\widehat {BEC} = 90^\circ \) Xét tứ giác \(BCEF\) có \(\widehat {BFC} = \widehat {BEC}\) (cùng bằng \(90^\circ \)), mà hai góc này cùng nhìn cạnh \(BC\) Do đó tứ giác \(BCEF\) nội tiếp. Suy ra \(\widehat {BCE} = \widehat {HFE}\) (cùng phụ với \(\widehat {BFE}\)) \(\left( 1 \right)\) Vì \(BHEK\) là tứ giác nội tiếp nên \(\widehat {BHK} = \widehat {BEK}\) (hai góc nội tiếp cùng chắn cung \(BK\)). \[\left( 2 \right)\] Xét \(\Delta HEF\) vuông tại \(H\) có \(HI\) là đường trung tuyến ứng với cạnh huyền \(EF\) nên \(IH = IF = IE = \frac{1}{2}EF\). Suy ra tam giác \(FHI\) cân tại \(I\), do đó \(\widehat {HFE} = \widehat {FHI}\) \[\left( 3 \right)\] Mặt khác \(\widehat {BEK} = \widehat {BCE}\) (vì cùng phụ với \(\widehat {EBC}\)) \[\left( 4 \right)\] Từ (1), (2), (3), (4) suy ra \(\widehat {BHK} = \widehat {FHI}\). Do tam giác \(ABC\) nhọn, hai điểm \(I,K\) nằm cùng phía đối với đường thẳng \(HF\) nên là ba điểm thẳng hàng. |
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
|
Gọi tọa độ điểm \(A\) là \(\left( {{x_A};{y_A}} \right)\). Do điểm \(A\) thuộc trục \(Oy\)nên \({x_A} = 0\) DO điểm \(A\) thuộc đường thẳng \(\left( d \right):y = mx + 4\) nên \({y_A} = m{x_A} + 4 = m.0 + 4 = 4\). Kết luận tọa độ điểm \(A\) là \(\left( {0;4} \right)\). |
|
Tìm tất cả các giá trị của \[m\] để đường thẳng \[\left( d \right)\] cắt trục \[Ox\] tại điểm \[B\] sao cho \[OAB\] là tam giác cân. |
|
Gọi tọa độ điểm \(B\) là \(\left( {{x_B};{y_B}} \right)\). Do điểm \(B\) thuộc trục \(Ox\) nên \({y_B} = 0\). Vì điểm \(B\) thuộc đường thẳng \(\left( d \right):mx + 4\) nên \(0 = m{x_B} + 4\) Vì \(m \ne 0 \Rightarrow {x_B} = \frac{{ - 4}}{m} \Rightarrow OB = \left| {{x_B}} \right| = \left| {\frac{{ - 4}}{m}} \right|\). Vì \(\widehat {AOB} = 90^\circ \) nên để tam giác \(OAB\) là tam giác cân thì \(OA = OB\). Mà \(OA = 4\) nên \(OB = 4\). Giải phương trình: \(\left| {\frac{{ - 4}}{m}} \right| = 4 \Leftrightarrow \left[ \begin{array}{l}\frac{{ - 4}}{m} = 4\\\frac{{ - 4}}{m} = - 4\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}m = - 1\\m = 1\end{array} \right.\)(tmđk) Kết luận: \(m = 1\) hoặc \(m = - 1\). |
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập