Cho hàm số y= x4-2( m+1)x2+ m ( C). Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số C có ba điểm cực trị A: B; C sao cho OA= BC ; trong đó O là gốc tọa độ, A là điểm cực trị thuộc trục tung, B và C là hai điểm cực trị còn lại.
A.
B.
C.
D.
Quảng cáo
Trả lời:
Giải bởi Vietjack
Ta có : y’ = 4x3-4( m+ 1) x= 4x( x2- (m+ 1) ).
Hàm số có 3 điểm cực trị khi và chỉ khi y’ = 0 có 3 nghiệm phân biệt hay m + 1> 0 suy ra m > - 1. (*)
Khi đó, ta có:
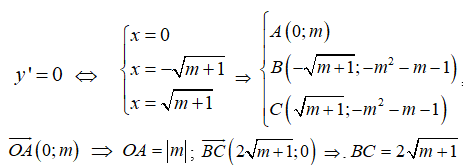
Do đó (thỏa mãn (*).
Vậy
Chọn A.
Hot: Danh sách các trường đã công bố điểm chuẩn Đại học 2025 (mới nhất) (2025). Xem ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Tập xác định D= R\ { 1}.
Đạo hàm
Đồ thị hàm số C có tiệm cận đứng là x= 1 và tiệm cận ngang y= 2 nên I (1 ;2 ) là giao của 2 đường tiệm cận.
Gọi
Tiếp tuyến ∆ của C tại M có phương trình là :
∆ cắt TCĐ tại và cắt TCN tại B( 2x0-1 ; 2) .
Ta có
Do đó, .
Chọn D.
Câu 2
A. m> 1
B. m< 1
C. m≤ -1
D. m≥ -1
Lời giải
Ta có:
Hàm số Y= ln( x2+ 1) –mx+1 đồng biến trên R khi và chỉ khi y’≥ 0 với mọi x.
Bảng biến thiên:
Dựa vào bảng biến thiên ta có: với mọi x khivà chỉ khi m≤ -1.
Chọn C.
Câu 3
A. m= 1.
B . m = 2
C. m= -2
D. Đáp án khác
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. x= 3 và x= - 2.
B. x= -3
C. x= 3và x= 2.
D. x= 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. 4
B. 3
C. 1
D. 2
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo