Câu hỏi trong đề: Bài tập ôn tập chương 3 hình học 9 có đáp án !!
Quảng cáo
Trả lời:
Cách dựng: ta lần lượt thực hiện:
- Dựng đoạn BC = a.
- Dựng cung chứa góc dựng trên đoạn thẳng BC.
- Dựng đường tròn đường kính BC.
- Dựng đường tròn (B, h) cắt đường tròn đường kính BC tại H.
- Tia CH cắt cung chứa góc tại A.
- Nối AB ta được phải dựng
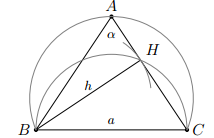
Chứng minh: ta có ngay:
- BC = a theo cách dựng.
- vì A nằm trên cung chứa góc dựng trên đoạn thẳng BC.
- BH = h vì H thuộc đường tròn (B, h)
- => Bh = h là đường cao của
Vậy thỏa mãn điều kiện đầu bài.
Biện luận: ta dựng dược hai tam giác ABC và A’BC thỏa mãn điều kiện đề bài, nhưng hai tam giác này bằng nhau (đối xứng qua BC) nên bài toán chỉ có một nghiệm hình.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
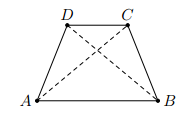
Xét hai tam giác và , ta có:
CD chung
, vì ABCD là hình thang cân.
AD = BC, vì ABCD là hình thang cân.
Do đó:
=>
Vậy các điểm A, B nằm cùng phía đối với CD và thỏa mãn nên bốn điểm A, B, C, D cùng thuộc một đường tròn.
Lời giải

- Phần thuận:
Xét hai tam giác vuông có
BC = CD (do ABCD là hình vuông)
CE = CF (gt) nên
Do đó,
Mà (đối đỉnh) nên
Vậy điểm M nằm trên đường tròn đường kính BD.
- Giới hạn:
+ Nếu
+ Nếu
Vậy điểm M chỉ nằm trên cung nhỏ của đường tròn đường kính BD.
- Phần đảo:
Lấy điểm M trên cung nhỏ của đường tròn đường kính BD. Nối MB, MD lần lượt cắt CD, BC tại F, E
Ta có (góc nội tiếp chắn nửa đường tròn) nên do đó CF = CE.
- Kết luận: quỹ tích điểm M nằm trên cung nhỏ của đường tròn đường kính BD.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.