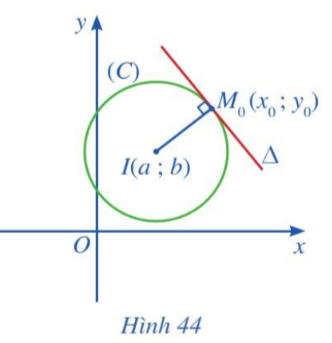
Cho điểm M0(x0; y0) nằm trên đường tròn (C) tâm I(a; b) bán kính R. Gọi ∆ là tiếp tuyến tại điểm M0(x0; y0) thuộc đường tròn (Hình 44). Chứng tỏ rằng ( overrightarrow {I{M_0}} ) là vectơ pháp tuyến c...

Câu hỏi:

04/07/2022 1,251

Cho điểm M₀(x₀; y₀) nằm trên đường tròn (C) tâm I(a; b) bán kính R.

Gọi ∆ là tiếp tuyến tại điểm M₀(x₀; y₀) thuộc đường tròn (Hình 44).

Chứng tỏ rằng \(\overrightarrow {I{M_0}} \) là vectơ pháp tuyến của đường thẳng ∆.

Xem lời giải

Câu hỏi trong đề: Bài tập Phương trình đường tròn có đáp án !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

Hướng dẫn giải

Vì đường thẳng ∆ là tiếp tuyến của đường tròn (C) có tâm I tại điểm M₀ nên IM₀ vuông góc với ∆ tại M₀ (tiếp tuyến của đường tròn vuông góc với bán kính đi qua tiếp điểm).

Do đó, vectơ \(\overrightarrow {I{M_0}} \) có giá là đường thẳng IM₀ vuông góc với đường thẳng ∆.

Vậy vectơ \(\overrightarrow {I{M_0}} \) là vectơ pháp tuyến của đường thẳng ∆.

Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

Bình luận

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Ném đĩa là một môn thể thao thi đấu trong Thế vận hội Olympic mùa hè. Khi thực hiện cú ném, vận động viên thường quay lưng lại với hướng ném, sau đó xoay ngược chiều kim đồng hồ một vòng rưỡi của đường tròn để lấy đà rồi thả tay ra khỏi đĩa. Giả sử đĩa chuyển động trên một đường tròn tâm \(I\left( {0;\,\frac{3}{2}} \right)\) bán kính 0,8 trong mặt phẳng tọa độ Oxy (đơn vị trên hai trục là mét). Đến điểm \(M\left( {\frac{{\sqrt {39} }}{{10}};\,\,2} \right)\), đĩa được ném đi (Hình 47). Trong những giây đầu tiên ngay sau khi được ném đi, quỹ đạo chuyển động của chiếc đĩa có phương trình như thế nào?

Xem đáp án

Lời giải

Hướng dẫn giải

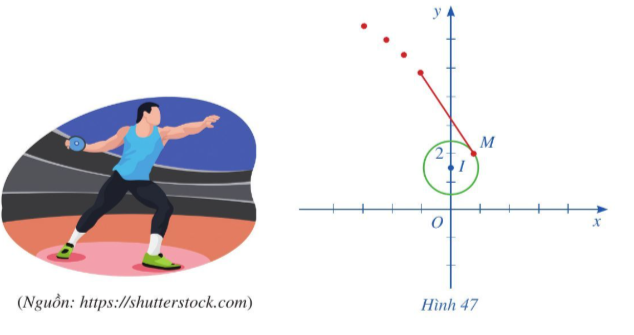
Đĩa chuyển động trên một đường tròn tâm \(I\left( {0;\,\frac{3}{2}} \right)\) bán kính 0,8; đến điểm \(M\left( {\frac{{\sqrt {39} }}{{10}};\,\,2} \right)\), đĩa được ném đi, do đó trong những giây đầu tiên sau khi ném đi, đĩa chuyển động trên một đường thẳng là tiếp tuyến của đường tròn tâm I, bán kính 0,8 tại tiếp điểm M.

Phương trình tiếp tuyến của đường tròn tâm I tại tiếp điểm M là

\(\left( {\frac{{\sqrt {39} }}{{10}} - 0} \right)\left( {x - \frac{{\sqrt {39} }}{{10}}} \right) + \left( {2 - \frac{3}{2}} \right)\left( {y - 2} \right) = 0\)

\( \Leftrightarrow \frac{{\sqrt {39} }}{{10}}x - \frac{{39}}{{100}} + \frac{1}{2}y - 1 = 0\)

\( \Leftrightarrow 10\sqrt {39} x + 50y - 139 = 0\).

Vậy trong những giây đầu tiên ngay sau khi được ném đi, quỹ đạo chuyển động của chiếc đĩa có phương trình là \(10\sqrt {39} x + 50y - 139 = 0\).

Câu 2

Tìm m sao cho đường thẳng 3x + 4y + m = 0 tiếp xúc với đường tròn

(x + 1)2 + (y – 2)2 = 4.

Xem đáp án

Lời giải

Hướng dẫn giải

Ta có: (x + 1)² + (y – 2)² = 4 ⇔ (x – (– 1))² + (y – 2)² = 2².

Đường tròn đã cho có tâm I(– 1; 2) và bán kính R = 2.

Gọi đường thẳng d có phương trình 3x + 4y + m = 0, đường thẳng này tiếp xúc với đường tròn đã cho khi và chỉ khi khoảng cách từ tâm I của đường tròn đến đường thẳng bằng bán kính của đường tròn hay d(I, d) = R

\( \Leftrightarrow \frac{{\left| {3.\left( { - 1} \right) + 4.2 + m} \right|}}{{\sqrt {{3^2} + {4^2}} }} = 2\)

\( \Leftrightarrow \frac{{\left| {m + 5} \right|}}{5} = 2\) ⇔ |m + 5| = 10

Suy ra m + 5 = 10 hoặc m + 5 = – 10

Suy ra m = 5 hoặc m = – 15.

Vậy m = 5, m = – 15 thì thỏa mãn yêu cầu bài toán.

Câu 3