Câu hỏi:
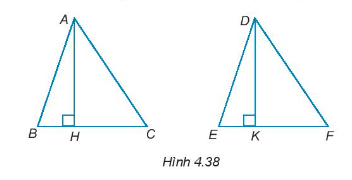
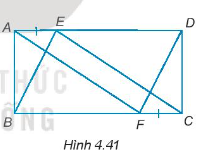
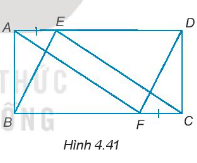
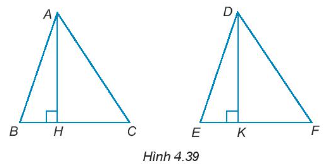
12/07/2024 361Cho AH và DK lần lượt là hai đường cao của tam giác ABC và DEF như Hình 4.39. Chứng minh rằng:
Nếu AB = DE, AC = DF và AH = DK thì ∆ABC = ∆DEF.
Quảng cáo
Trả lời:
Giải bởi Vietjack
Hướng dẫn giải
Vì AH là đường cao của tam giác ABC nên AH vuông góc với BC. Do đó, \(\widehat {AHB} = \widehat {AHC} = 90^\circ \).
Vì DK là đường cao của tam giác DEF nên DK vuông góc với EF. Do đó, \(\widehat {DKE} = \widehat {DKF} = 90^\circ \).
Xét ∆ABH và ∆DEK có:
\(\widehat {AHB} = \widehat {DKE} = 90^\circ \) (chứng minh trên)
AB = DE (giả thiết)
AH = DK (giả thiết)
Do đó, ∆ABH = ∆DEK (cạnh huyền – cạnh góc vuông).
Suy ra, BH = EK.
Xét ∆ACH và ∆DFK có:
\(\widehat {AHC} = \widehat {DKF} = 90^\circ \) (chứng minh trên)
AC = DF (giả thiết)
AH = DK (giả thiết)
Do đó, ∆ACH = ∆DFK (cạnh huyền – cạnh góc vuông).
Suy ra, CH = FK.
Ta có: BC = BH + HC; EF = EK + FK. Mà BH = EK; HC = FK nên BC = EF.
Xét ∆ABC và ∆DEF có:
BC = EF (chứng minh trên)
AC = DF (giả thiết)
AB = DE (giả thiết)
Do đó, ∆ABC = ∆DEF (c – c – c).
Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay
Sách thầy cô Vietjack biên soạn:
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Hướng dẫn giải
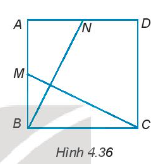
Vì ABCD là hình vuông nên AB = BC = CD = DA.
Vì N là trung điểm của AD nên AN = ND = \(\frac{{AD}}{2}\).
Vì M là trung điểm của AB nên AM = MB = \(\frac{{AB}}{2}\).
Mà AB = AD nên AN = BM.
Xét ∆ANB và ∆BMC có:
AN = BM (chứng minh trên)
AB = BC (chứng minh trên)
\(\widehat {NAB}\) = \(\widehat {MBC}\) = 90° (do ABCD là hình vuông)
Do đó, ∆ANB = ∆BMC (hai cạnh góc vuông)
Suy ra, BN = CM (hai cạnh tương ứng).
Gọi E là giao điểm của BN và CM.
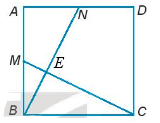
Do ∆ANB = ∆BMC nên \(\widehat {EMB} = \widehat {CMB} = \widehat {BNA}\).
Từ định lí tổng ba góc trong tam giác BME và tam giác ABN, ta suy ra:
\(\widehat {BEM} = 180^\circ - \widehat {EMB} - \widehat {MBE} = 180^\circ - \widehat {BNA} - \widehat {ABN} = \widehat {BAN} = 90^\circ \).
Vậy BN vuông góc với CM tại E.
Lời giải
Hướng dẫn giải
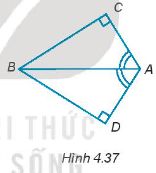
Xét ∆ABC và ∆ABD có:
AB chung
\(\widehat {CAB}\) = \(\widehat {DAB}\) (giả thiết)
\(\widehat {ACB}\) = \(\widehat {ADB}\) = 90° (giả thiết)
Do đó, ∆ABC = ∆ABD (cạnh huyền – góc nhọn).
Suy ra CB = DB.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
Đề kiểm tra cuối học kỳ 2 Toán 7 Kết nối tri thức có đáp án - Đề 1
-
Đề kiểm tra cuối học kỳ 2 Toán 7 Kết nối tri thức có đáp án - Đề 2
-
Bộ 7 đề thi học kì 2 Toán lớp 7 Chân trời sáng tạo có đáp án - Đề 04
-
15 câu Trắc nghiệm Toán 7 Kết nối tri thức Bài 1: Tập hợp các số hữu tỉ có đáp án
-
Bộ 7 đề thi học kì 2 Toán 7 Cánh Diều có đáp án - Đề 01
-
Bộ 7 đề thi học kì 2 Toán lớp 7 Chân trời sáng tạo có đáp án - Đề 01
-
Bộ 7 đề thi học kì 2 Toán 7 Cánh Diều có đáp án - Đề 02
-
Bộ 7 đề thi học kì 2 Toán lớp 7 Chân trời sáng tạo có đáp án - Đề 02
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận