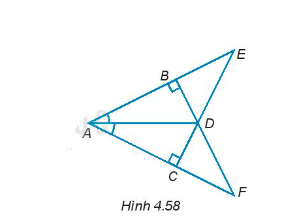
Cho các điểm A, B, C, D, E, F như Hình 4.58.

Tìm ba cặp tam giác vuông bằng nhau và giải thích vì sao chúng bằng nhau.

Hướng dẫn giải

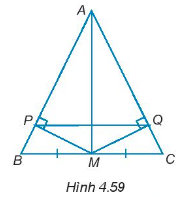
a) Xét tam giác vuông PBM và tam giác vuông QCM có:

BM = MC (do M là trung điểm của BC)

\(\widehat B = \widehat C\) (do tam giác ABC cân tại đỉnh A)

Do đó, ∆PBM = ∆QCM (cạnh huyền – góc nhọn).

Suy ra MP = MQ.

Ta lại có: AB = AC (do tam giác ABC cân tại đỉnh A).

AB = AP + PB, AC = AQ + QC.

Suy ra AP + PB = AQ + QC

Mà PB = QC (do ∆PBM = ∆QCM)

Do đó AP = AQ.

Hướng dẫn giải

a) Câu a) đúng.

Giải thích:

+ Giả sử tam giác ABC cân tại đỉnh A có góc ở đáy \(\widehat B\) = 60°.

Khi đó, \(\widehat C = \widehat B = 60^\circ \).

Theo định lí tổng ba góc trong tam giác, ta có: \(\widehat A + \widehat B + \widehat C = 180^\circ \).

\( \Rightarrow \widehat A = 180^\circ - \widehat B - \widehat C = 180^\circ - 60^\circ - 60^\circ = 60^\circ \).

Do đó, \(\widehat A = \widehat B = \widehat C = 60^\circ \), nên tam giác ABC cân tại đỉnh C.

Vậy tam giác ABC đều.

+ Giả sử tam giác ABC cân tại đỉnh A có góc ở đỉnh \(\widehat A = 60^\circ \).

Theo định lí tổng ba góc trong tam giác, ta có: \(\widehat A + \widehat B + \widehat C = 180^\circ \).

Mà \(\widehat B = \widehat C\) (do tam giác ABC cân đỉnh A).

Do đó, \(\widehat B + \widehat B = 180^\circ - \widehat A = 180^\circ - 60^\circ = 120^\circ \), suy ra \(\widehat B = 60^\circ \).

Do đó, \(\widehat A = \widehat B = \widehat C = 60^\circ \), nên tam giác ABC cân tại đỉnh C.

Vậy tam giác ABC đều.

b) Câu b) sai.

Chẳng hạn tam giác ABC cân tại đỉnh A có \(\widehat A = 100^\circ \), \(\widehat B = \widehat C = 40^\circ \), đây là tam giác tù.

c) Từ định lí tổng ba góc trong tam giác, ta suy ra tổng hai góc nhọn của một tam giác vuông bằng 90°.

Vậy câu c) đúng.

d) Tam giác vuông cân thì luôn cân tại đỉnh góc vuông và có hai góc nhọn bằng 45° là câu đúng.

Giả sử có tam giác ABC vuông tại A, cân tại B, khi đó \(\widehat A = \widehat C = 90^\circ \), do đó \(\widehat A + \widehat B + \widehat C > 180^\circ \) không thỏa mãn định lí tổng ba góc trong tam giác.

Vậy tam giác vuông cân thì luôn cân tại đỉnh góc vuông và từ định lí tổng ba góc và tính chất của tam giác cân, ta tính được số đo hai góc nhọn bằng 45°.

Vậy câu a), c), d) đúng và câu b) sai.