Câu hỏi:
13/07/2024 813
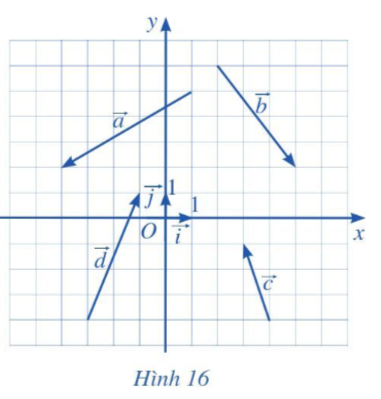
Tìm điểm M sao cho \(\overrightarrow {OM} = \overrightarrow {AB} \). Từ đó, tìm hoành độ a và tung độ b của vectơ \(\overrightarrow {AB} \).
Câu hỏi trong đề: Bài tập Tọa độ của vectơ có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Hướng dẫn giải:
Để xác định điểm M, ta làm như sau:
- Từ đểm O, kẻ đường thẳng d song song với giá của vectơ \(\overrightarrow {AB} \) (chính là đường thẳng AB).
- Lấy điểm M trên đường thẳng d sao cho hai vectơ \(\overrightarrow {AB} ,\,\,\overrightarrow {OM} \) cùng hướng và độ dài đoạn thẳng OM bằng độ dài vectơ \(\overrightarrow {AB} \) (chính là độ dài đoạn thẳng AB).
Ta xác định được điểm M thỏa mãn \(\overrightarrow {OM} = \overrightarrow {AB} \) như hình vẽ:
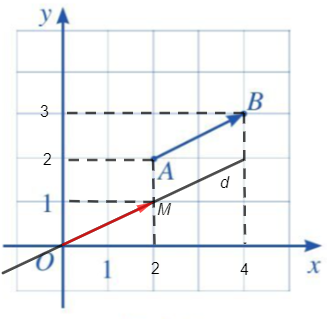
Từ điểm M, kẻ đường thẳng vuông góc với trục hoành, đường thẳng này cắt trục hoành tại điểm ứng với số 2, nên hoành độ của điểm M là xM = 2.
Từ điểm M, kẻ đường thẳng vuông góc với trục tung, đường thẳng này cắt trục tung tại điểm ứng với số 1, nên tung độ của điểm M là yM = 1.
Tọa độ của điểm M chính là tọa độ của vectơ \(\overrightarrow {OM} \) nên \(\overrightarrow {OM} = \left( {2;\,\,1} \right)\).
Lại có \(\overrightarrow {OM} = \overrightarrow {AB} \), do đó tọa độ của vectơ \(\overrightarrow {AB} \) là (2; 1).
Vậy hoành độ của vectơ \(\overrightarrow {AB} \) là a = 2 và tung độ của vectơ \(\overrightarrow {AB} \) là b = 1.
Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay
Sách thầy cô Vietjack biên soạn:
Sách - Sổ tay kiến thức trọng tâm Vật lí 10 VietJack - Sách 2025 theo chương trình mới cho 2k9
Đã bán 121
₫ 110.000
₫ 31.000
Trọng tâm Toán, Văn, Anh 10 cho cả 3 bộ KNTT, CTST, CD VietJack - Sách 2025
Đã bán 100
₫ 40.500
₫ 13.600
Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack
Đã bán 218
₫ 130.000
₫ 75.000
Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack
Đã bán 1k
₫ 104.000
₫ 52.000
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Trong mặt phẳng toạ độ Oxy, cho tam giác ABC. Các điểm M(1; – 2), N(4; – 1) và P(6; 2) lần lượt là trung điểm của các cạnh BC, CA, AB. Tìm tọa độ của các điểm A, B, C.
Xem đáp án »
11/07/2024
16,427
Câu 2:
Trong mặt phẳng toạ độ Oxy, cho ba điểm không thẳng hàng A(– 3; 1), B(– 1; 3), I(4; 2). Tìm toạ độ của hai điểm C, D sao cho tứ giác ABCD là hình bình hành nhận I làm tâm đối xứng.
Xem đáp án »
11/07/2024
8,593
Câu 3:
Trong mặt phẳng toạ độ Oxy, cho ba điểm A(2; 3), B(– 1; 1), C(3; – 1).
Tìm toạ độ điểm M sao cho \(\overrightarrow {AM} = \overrightarrow {BC} \).
Xem đáp án »
11/07/2024
8,592
Câu 4:
Tìm các số thực a và b sao cho mỗi cặp vectơ sau bằng nhau:
\(\overrightarrow u = \left( {2a - 1; - 3} \right)\) và \(\overrightarrow v = \left( {3;\,4b + 1} \right)\);
Xem đáp án »
11/07/2024
6,421
Câu 6:
Biểu diễn vectơ \(\overrightarrow {OB} \) qua hai vectơ \(\overrightarrow i \) và \(\overrightarrow j \).
Biểu diễn vectơ \(\overrightarrow {OB} \) qua hai vectơ \(\overrightarrow i \) và \(\overrightarrow j \).
Xem đáp án »
13/07/2024
4,109
Câu 7:
\(\overrightarrow x = \left( {a + b;\,\, - 2a + 3b} \right)\) và \(\overrightarrow y = \left( {2a - 3;\,\,4b} \right)\).
Xem đáp án »
13/07/2024
3,226
🔥 Đề thi HOT:
-
10 Bài tập Ứng dụng ba đường conic vào các bài toán thực tế (có lời giải)
-
13 câu Trắc nghiệm Tích của vectơ với một số có đáp án (Thông hiểu)
-
12 Bài tập Ứng dụng của hàm số bậc hai để giải bài toán thực tế (có lời giải)
-
185 câu Trắc nghiệm Toán 10 Bài 1:Phương trình đường thẳng trong mặt phẳng oxy có đáp án (Mới nhất)
-
Bộ 5 đề thi cuối kì 2 Toán 10 Kết nối tri thức cấu trúc mới có đáp án - Đề 1
-
16 câu Trắc nghiệm Toán 10 Kết nối tri thức Mệnh đề có đáp án
-
Bộ 2 Đề kiểm tra giữa học kì 2 Toán 10 Kết nối tri thức có đáp án - Đề 1
-
10 Bài tập Các bài toán thực tế ứng dụng nhị thức Newton (có lời giải)
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận