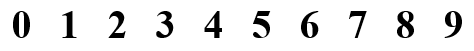Bộ 5 đề thi cuối kì 1 Toán 6 Kết nối tri thức (Tự luận) có đáp án - Đề 2

Hướng dẫn giải

Hướng dẫn giải

2. Để \(\overline {71a1b} \) chia hết cho 45 thì \(\overline {71a1b} \) chia hết cho 5 và 9.

Vì \(\overline {71a1b} \,\, \vdots \,\,5\) nên \(b \in \left\{ {0\,;\,\,5} \right\}\).

Vì \(\overline {71a1b} \,\, \vdots \,\,9\) thì \[\left( {7 + 1 + a + 1 + b} \right)\,\, \vdots \,\,9\] hay \[\left( {9 + a + b} \right)\,\, \vdots \,\,9\].

Với \(b = 0\) thì \[\left( {9 + a + 0} \right)\,\, \vdots \,\,9\] nên \(a \in \left\{ {0\,;\,\,9} \right\}.\)

Với \(b = 5\) thì \[\left( {9 + a + 5} \right)\,\, \vdots \,\,9\] nên \(a = 4.\)

Vậy để \(\overline {71a1b} \) chia hết cho 45 thì cặp số \[\left( {a;\,\,b} \right)\] lần lượt là \[\left( {0\,;\,\,0} \right)\,;\,\,\left( {9\,;\,\,0} \right)\,;\,\,\left( {4\,;\,\,5} \right).\]

Hướng dẫn giải

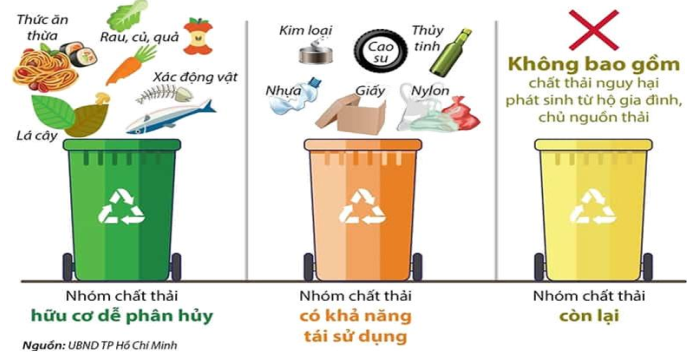
1. Tập hợp \(B\) gồm các loại chất thải hữu cơ dễ phân hủy là:

\(B = \{ \)Thức ăn thừa; rau; củ; quả; lá cây; xác động vật}.

2. Sau 3 giờ, ô tô đi đến B thì đi được: \(42 \cdot 3 = 126\,\,\left( {{\rm{km}}} \right).\)

Sau 3 giờ, ô tô đi đến C thì đi được: \( - 45 \cdot 3 = - 135\,\,\left( {{\rm{km}}} \right).\)

Khoảng cách giữa hai ô tô là: \(126 - \left( { - 135} \right) = 261\,\,\left( {{\rm{km}}} \right).\)

Vậy nếu hai ô tô đi với vận tốc lần lượt là \(42\,\,{\rm{km/}}\,{\rm{h}}\) và \( - 45\,\,{\rm{km/}}\,{\rm{h}}\) thì sau 3 giờ hai ô tô cách nhau \(261\,\,{\rm{km}}.\)

3. Gọi số bó hoa mà cửa hàng bó được là x (bó, \(x \in \mathbb{N}*\)).

Theo bài ta có: \(144\,\, \vdots \,\,x,\,\,120\,\, \vdots \,\,x,\,\,96\,\, \vdots \,\,x\) và x là số bó hoa nhiều nhất cửa hàng bó.

Nên x là ƯCLN(144, 120, 96).

Ta có: \(144 = {2^4}{.3^2}\); \(120 = {2^3}.3.5\); \(96 = {2^5}.3\)

Suy ra \(x = \) ƯCLN\[\left( {144,120,96} \right) = {2^3}.3 = 24\]

Khi đó, mỗi bó có \[144:24 = 6\] bông hoa hồng đỏ;

\[120:24 = 5\] bông hoa hồng phấn;

\[96:24 = 4\] bông hoa hồng vàng.

Vậy cửa hàng bó được nhiều nhất 24 bó, khi đó mỗi bó có 6 bông hoa hồng đỏ, 5 bông hoa hồng phấn và 4 bông hoa hồng vàng.

Hướng dẫn giải

1. a) Các số vừa có trục đối xứng, vừa có tâm đối xứng là số 0, 8.

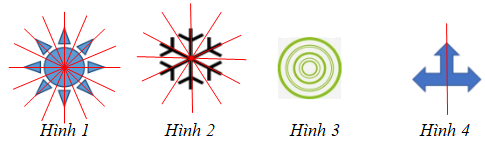
b) Hình 1 có 8 trục đối xứng;

Hình 2 có 6 trục đối xứng;

Hình 3 có vô số trục đối xứng là các đường kính của hình tròn.

Hình 4 có 1 trục đối xứng.

2. a) Diện tích một mặt của hộp giấy là: \(\frac{{\left( {10 + 13} \right).20}}{2} = 230\,\,\left( {{\rm{c}}{{\rm{m}}^{\rm{2}}}} \right)\).

Vậy diện tích một mặt bên của hộp giấy là \(230\,\,{\rm{c}}{{\rm{m}}^{\rm{2}}}.\)

b) Diện tích bốn mặt xung quanh của chiếc hộp là: \(230.\,4\,\, = \,\,920\,\,\left( {{\rm{c}}{{\rm{m}}^{\rm{2}}}} \right)\)

Đáy hộp đựng bỏng ngô là hình vuông nên có diện tích là: \(10.\,10 = \,100\,\,\left( {{\rm{c}}{{\rm{m}}^{\rm{2}}}} \right)\)

Diện tích giấy bìa ít nhất để làm được một chiếc hộp là: \(920\, + \,100\,\, = \,1020\,\,\left( {{\rm{c}}{{\rm{m}}^{\rm{2}}}} \right)\).

Vậy cần ít nhất \(1020\,\,{\rm{c}}{{\rm{m}}^{\rm{2}}}\) giấy bìa để làm một chiếc hộp đựng bỏng ngô đó.