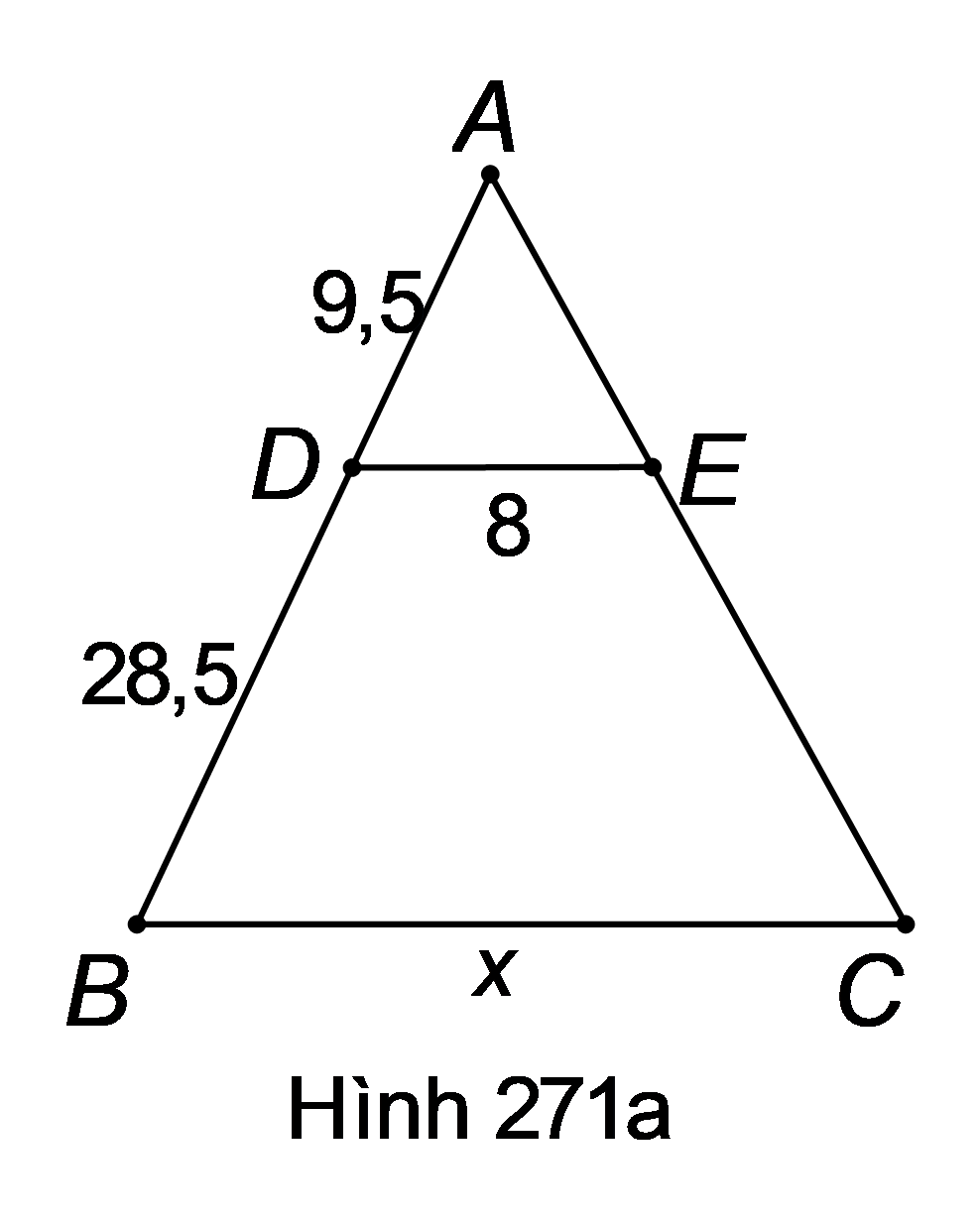Quảng cáo
Trả lời:
Giải bởi Vietjack
Áp dụng hệ quả của định lí Ta-lét cho , ta được:
hay
.
Hot: 1000+ Đề thi cuối kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
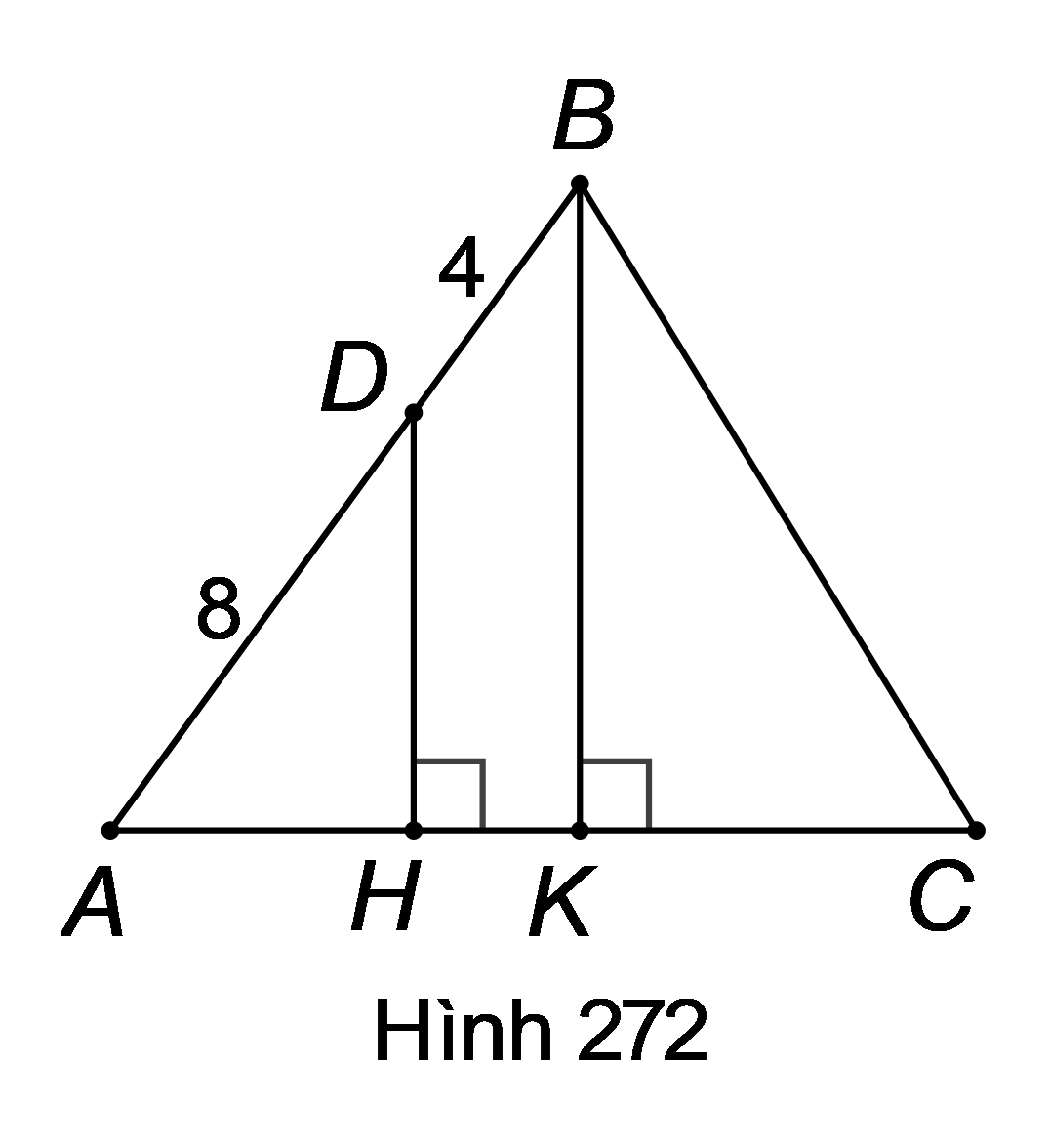
Kẻ DH và BK cùng vuông góc với AC thì và lần lượt là khoảng cách từ các điểm D và B đến cạnh AC.
Áp dụng hệ quả của định lí Ta-lét cho thu được hay .
Lời giải
Có hai cách chia một đoạn AB cho trước thành 5 phần bằng nhau.
Cách 1: Sử dụng hệ quả của định lí Ta-lét.
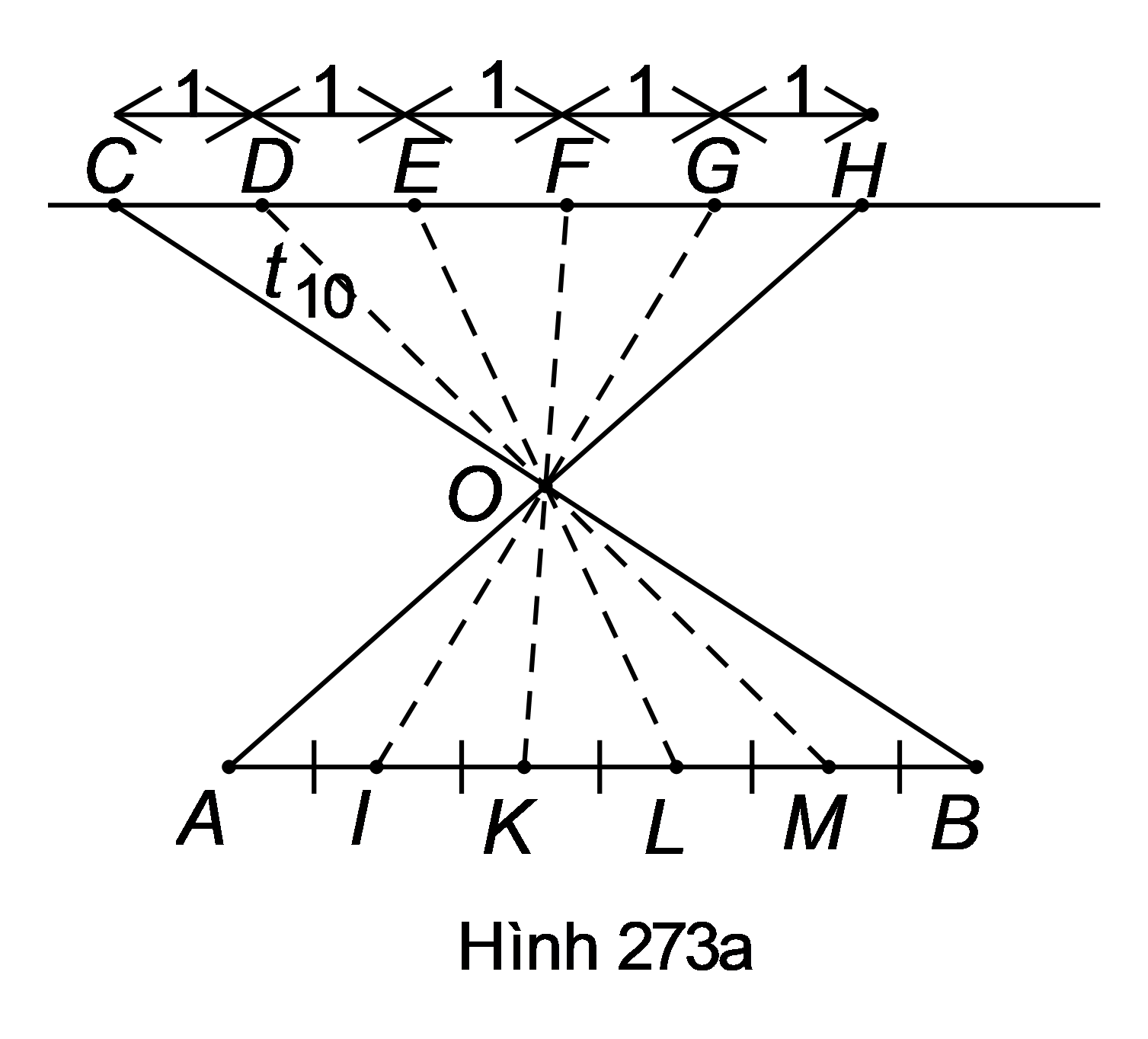
Kẻ đường thẳng .
Từ điểm C bất kì trên a, đặt liên tiếp các đoạn thẳng bằng nhau:
.
Gọi O là giao điểm của AH và BC.
Vẽ các đường thẳng cắt AB theo thứ tự ở thì các điểm này chia đoạn AB thành 5 phần bằng nhau. Thật vậy:
Áp dụng hệ quả của định lí Ta-lét cho , ta được:
do .
Chứng minh tương tự, ta được: .
Cách 2: Sử dụng tính chất của đường thẳng song song cách đều.
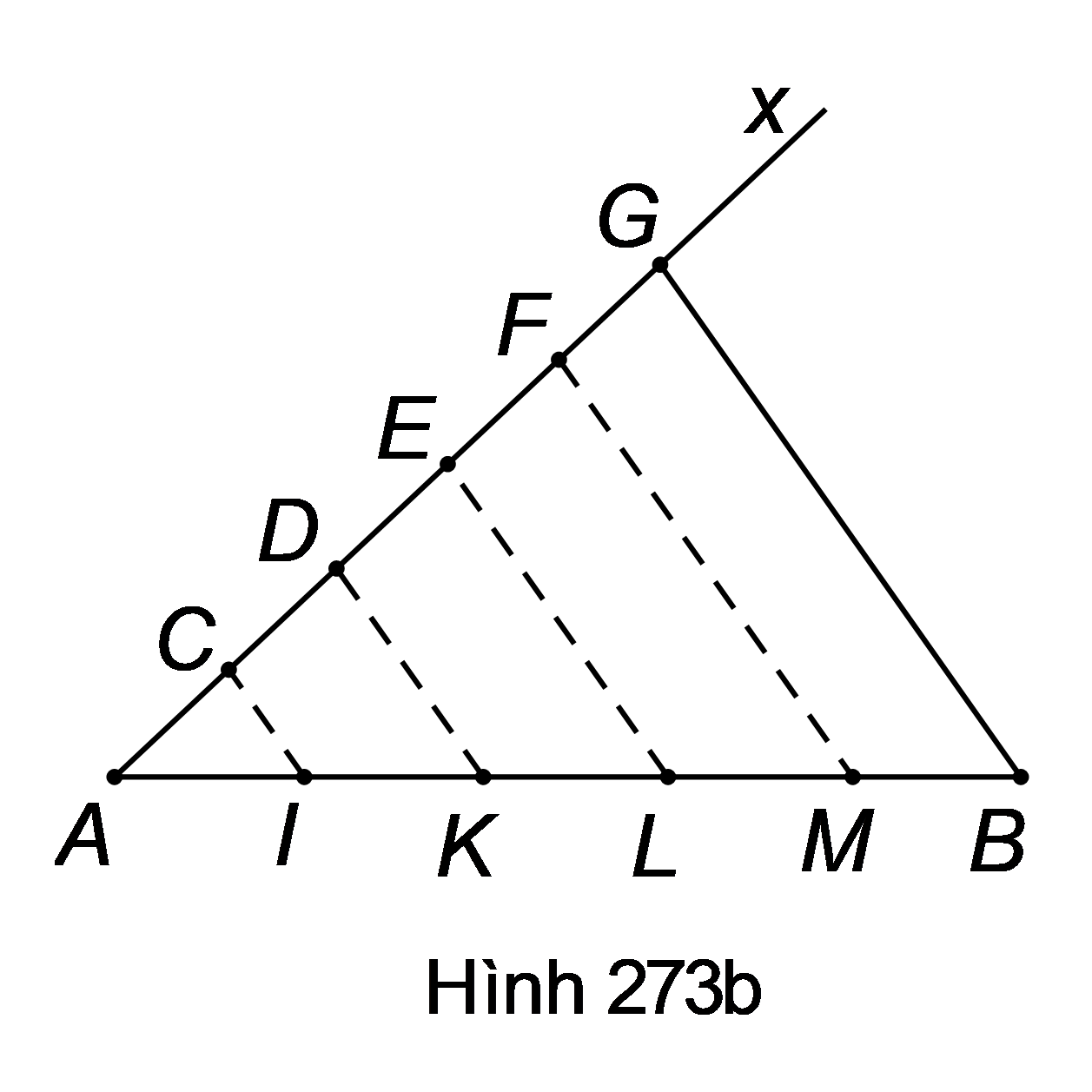
Kẻ tia Ax, trên đó đặt liên tiếp các đoạn thẳng bằng nhau:
.
Nối GB. Từ kẻ các đường thẳng song song với GB, chúng cắt AB lần lượt ở thì CI, là năm đường thẳng song song cách đều nên chúng chắn trên đường thẳng AB những đoạn
thẳng liên tiếp bằng nhau là .
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập