Câu hỏi:

13/07/2024 4,437

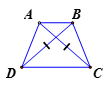
Cho hình thang cân ABCD (AB //CD) có hai đường chéo cắt nhau tại O. Chứng minh OA = OB, OC = OD.

Xem lời giải

Câu hỏi trong đề: Bài tập Toán 8 Chủ đề 3: Hình thang cân có đáp án !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

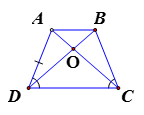
Cho hình thang cân ABCD (AB //CD) có hai đường chéo cắt nhau tại O. Chứng minh OA = OB, OC = OD. (ảnh 1)

Xét hai tam giác BDC và ACD có: cạnh DC chung; $\hat{B C D} = \hat{A D C}$ và AD = BC (tính chất hình thang cân)

$\Rightarrow Δ B D C = Δ A C D$ (c-g-c)

$\Rightarrow \hat{B D C} = \hat{A C D}$

$\Rightarrow Δ O D C$ cân tại O => OD = OC

Chứng minh tương tự ta có OB = OC.

Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

Bình luận

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Cho tam giác ABC cân tại A . Trên tia đối của tia AB lấy điểm D; trên tia đối của tia AC lấy điểm E sao cho AD = AE. Tứ giác BCDE là hình gì? Vì sao?

Xem đáp án

Lời giải

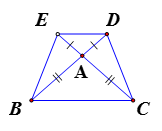
Cho tam giác ABC cân tại A . Trên tia đối của tia AB lấy điểm D ; trên tia đối của tia AC lấy điểm E sao cho AD = AE. (ảnh 1)

Theo giá thiết ta có các tam giác ABC và ADE là các tam giác cân nên $\hat{A E D} = \frac{180^{0} - \hat{E A D}}{2}$ và $\hat{A C B} = \frac{180^{0} - \hat{B A C}}{2}$

Mặt khác $\hat{E A D} = \hat{B A C}$ (đối đỉnh) nên $\hat{A E D} = \hat{A C B}$

Mà hai góc này ở vị trí so le trong nên DE // BC

=> BCDE là hình thang

Lại có EC = EA + AC = DA + AB = DB nên BCDE là hình thang cân.

Câu 2

Tứ giác ABCD có AB = BC = AD; $\hat{A} = 110^{0}$ ; $\hat{C} = 70^{0}$ . Chứng minh rằng:

a) DB là tia phân giác góc D.

Xem đáp án

Lời giải

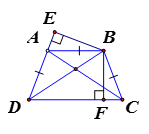
Tứ giác ABCD có AB = BC = AD ; góc A = 110 độ; góc C = 70 độ . Chứng minh rằng: a) DB là tia phân giác góc D. (ảnh 1)

a) Kẻ BE vuông góc với tia DA; BF vuông góc với tia DC

Khi đó do hai tam giác vuông BEA và BFCcó: $\hat{B A E} = \hat{B C F} = 70^{0}$ và AB = BC nên chúng bằng nhau. Do đó: BE = BF

=> B thuộc tia phân giác $\hat{A D C}$ hay DB là tia phân giác của $\hat{A D C}$ .

Câu 3

Cho hình thang cân ABCD (AB // CD) có $\hat{A} = 110^{0}$ . Tính các góc còn lại của hinh thang ABCD

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 4

Cho tam giác ABC cân tại A . Đường thẳng song song với BC cắt hai cạnh AB, AC lần lượt tại M, N. Chứng minh BCNM là hình thang cân.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 5

Cho hình thang cân ABCD (AB // CD) có các đường cao AE, BF. Chứng minh DE = CF.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 6

Trong các hình vẽ sau, hình nào là hình thang cân. Giải thích.

a) AB // CD

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Xem thêm các câu hỏi khác »

Hỏi bài tập

Đăng ký gói thi VIP

VIP +1 tháng ( 199,000 VNĐ )

VIP +1 - Luyện thi tất cả các đề có trên Website trong 1 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +3 tháng ( 299,000 VNĐ )

VIP +3 - Luyện thi tất cả các đề có trên Website trong 3 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +6 tháng ( 399,000 VNĐ )

VIP +6 - Luyện thi tất cả các đề có trên Website trong 6 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +12 tháng ( 499,000 VNĐ )

VIP +12 - Luyện thi tất cả các đề có trên Website trong 12 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

Cho hình thang cân ABCD (AB //CD) có hai đường chéo cắt nhau tại O. Chứng minh OA = OB, OC = OD.

Bình luận

Cho tam giác ABC cân tại A . Trên tia đối của tia AB lấy điểm D; trên tia đối của tia AC lấy điểm E sao cho AD = AE. Tứ giác BCDE là hình gì? Vì sao?

Tứ giác ABCD có AB = BC = AD; A^=1100; C^=700. Chứng minh rằng: a) DB là tia phân giác góc D.

Cho hình thang cân ABCD (AB // CD) có A^=1100. Tính các góc còn lại của hinh thang ABCD

Cho tam giác ABC cân tại A . Đường thẳng song song với BC cắt hai cạnh AB, AC lần lượt tại M, N. Chứng minh BCNM là hình thang cân.

Cho hình thang cân ABCD (AB // CD) có các đường cao AE, BF. Chứng minh DE = CF.

Trong các hình vẽ sau, hình nào là hình thang cân. Giải thích. a) AB // CD

VIP +1 tháng ( 199,000 VNĐ )

VIP +3 tháng ( 299,000 VNĐ )

VIP +6 tháng ( 399,000 VNĐ )

VIP +12 tháng ( 499,000 VNĐ )

🔥 Đề thi HOT:

CHỌN BỘ SÁCH BẠN MUỐN XEM

Đăng ký

Đăng nhập

Quên mật khẩu

Tứ giác ABCD có AB = BC = AD; $\hat{A} = 110^{0}$ ; $\hat{C} = 70^{0}$ . Chứng minh rằng:

a) DB là tia phân giác góc D.

Cho hình thang cân ABCD (AB // CD) có $\hat{A} = 110^{0}$ . Tính các góc còn lại của hinh thang ABCD

Trong các hình vẽ sau, hình nào là hình thang cân. Giải thích.

a) AB // CD