Câu hỏi:

12/07/2024 1,427

b) Chứng minh tứ giác BDEC nội tiếp đường tròn.

Xem lời giải

Câu hỏi trong đề: Bài tập Toán 9 Chủ đề 3: Tứ giác nội tiếp có đáp án !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

b) Ta có: $\hat{B A H}$ = $\hat{C}$ (góc có cạnh tương ứng vuông góc) mà $\hat{D A H} = \hat{A D E}$ (1)

(Vì $A D H E$ là hình chữ nhật) => $\hat{C} = \hat{A D E}$ do $\hat{C} + \hat{B D E} = 180^{o}$ nên tứ giác $B D E C$ nội tiếp đường tròn.

Lưu ý: Có thể hướng dẫn học sinh một cách sử dụng hệ thức lượng và tam giác đồng dạng như sau:

Tam giác AHB vuông tại H, đường cao AH. Ta có $A H^{2} = A D . A B$

Tam giác AHC vuông tại H, đường cao AE. Ta có $A H^{2} = A E . A C$

Ta có $A D . A B = A E . A C \Rightarrow \frac{A D}{A C} = \frac{A E}{A B}$

Xét tam giác ADE và tam giác ACB có $\frac{A D}{A C} = \frac{A E}{A B}$ , $\hat{B A C} = \hat{D A E} = 90^{0}$ (góc chung)

$\Rightarrow Δ A D E Δ A C B$ $\Rightarrow \hat{A D E} = \hat{A C B}$ mà $\hat{A D E} + \hat{E D B} = 180^{0}$ nên $\hat{A D E} + \hat{E C B} = 180^{0}$

Tứ giác BDEC có $\hat{A D E} + \hat{E C B} = 180^{0}$ nên tứ giác BDEC nội tiếp đường tròn.

Hot: 500+ Đề thi vào 10 file word các Sở Hà Nội, TP Hồ Chí Minh có đáp án 2025 (chỉ từ 100k). Tải ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Cho đường tròn tâm O và điểm A nằm ngoài đường tròn. Kẻ hai tiếp tuyến AB, AC với đường tròn (B, C) là tiếp điểm. Trên cung nhỏ BC lấy một điểm M rồi kẻ các đường vuông góc MI, MH, MK xuống các cạnh BC, CA, AB. Gọi giao điểm của BM và IK là P; giao điểm của CM, IH là Q.

a) Chứng minh rằng các tứ giác BIMK, CIMH nội tiếp được;

Xem đáp án

Lời giải

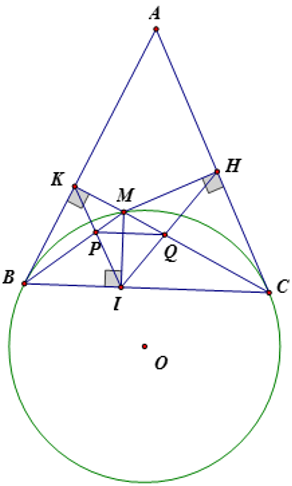
Cho đường tròn tâm O và điểm A nằm ngoài đường tròn. Kẻ hai tiếp tuyến AB, AC với đường tròn (B, C) là tiếp điểm. (ảnh 1)

* $\hat{B I M} = \hat{B K M} = 90^{0}$ suy ra tứ giác BIMK nội tiếp. (phương pháp 1)

* $\hat{C I M} = \hat{C H M} = 90^{0}$ suy ra tứ giác CIMH nội tiếp. (phương pháp 1)

Câu 2

Ta có : Tứ giác ABCD nội tiếp (O) Ta phải chứng minh: AC. BD = AB. DC + AD. BC

Xem đáp án

Lời giải

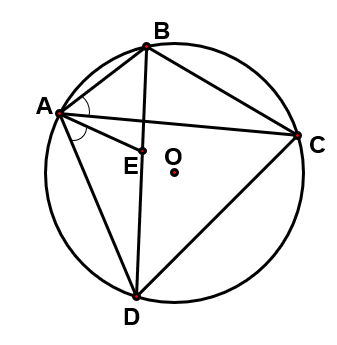
Ta có : Tứ giác ABCD nội tiếp (O) Ta phải chứng minh: AC. BD = AB. DC + AD. BC (ảnh 1)

Lấy E Î BD sao cho

Þ $Δ D A E Δ C A B$ (g. g)

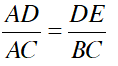
Þ Ta có : Tứ giác ABCD nội tiếp (O) Ta phải chứng minh: AC. BD = AB. DC + AD. BC (ảnh 2)

Þ AD. BC = AC. DE (1)

Tương tự: (g. g)

Þ $\frac{B E}{C D} = \frac{A B}{A C}$

Þ BE. AC = CD. AB (2)

Từ (1) và (2) Þ AD. BC + AB. CD = AC. DE + EB. AC

Þ AD. BC + AB. CD = AC. DB (đpcm)

Câu 3

b, Chứng minh MI² = MH.MK;

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 4

Cho nữa đường tròn tâm O đường kính AB , kẻ tiếp tuyến Bx và lấy hai điểm C và D thuộc nửa đường tròn. Các tia AC và AD cắt Bx lần lượt ở E, F ( F ở giữa B và E)

1. Chứng minh: $\hat{A B D} = \hat{D F B}$ .

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 5

Cho nửa đường tròn đường kính BC=2R. Từ điểm A trên nửa đường tròn vẽ $A H ⊥ B C$ . Nửa đường tròn đường kính BH, CH lần lượt có tâm $O_{1}$ ; $O_{2}$ cắt $A B$ và CA thứ tự tại D và E.

a) Chứng minh tứ giác $A D H E$ là hình chữ nhật, từ đó tính DE biết $R = 25$ và $B H = 10$

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 6

Cho tam giác ABC, 2 đường cao BB’, CC’. Chứng minh tứ giác BCB’C’ nội tiếp.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Xem thêm các câu hỏi khác »

Hỏi bài tập

Đăng ký gói thi VIP

VIP +1 tháng ( 199,000 VNĐ )

VIP +1 - Luyện thi tất cả các đề có trên Website trong 1 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +3 tháng ( 299,000 VNĐ )

VIP +3 - Luyện thi tất cả các đề có trên Website trong 3 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +6 tháng ( 399,000 VNĐ )

VIP +6 - Luyện thi tất cả các đề có trên Website trong 6 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +12 tháng ( 499,000 VNĐ )

VIP +12 - Luyện thi tất cả các đề có trên Website trong 12 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

b) Chứng minh tứ giác BDEC nội tiếp đường tròn.

Ta có : Tứ giác ABCD nội tiếp (O) Ta phải chứng minh: AC. BD = AB. DC + AD. BC

b, Chứng minh MI2 = MH.MK;

Cho nữa đường tròn tâm O đường kính AB , kẻ tiếp tuyến Bx và lấy hai điểm C và D thuộc nửa đường tròn. Các tia AC và AD cắt Bx lần lượt ở E, F ( F ở giữa B và E) 1. Chứng minh:ABD^=DFB^ .

Cho tam giác ABC, 2 đường cao BB’, CC’. Chứng minh tứ giác BCB’C’ nội tiếp.

VIP +1 tháng ( 199,000 VNĐ )

VIP +3 tháng ( 299,000 VNĐ )

VIP +6 tháng ( 399,000 VNĐ )

VIP +12 tháng ( 499,000 VNĐ )

🔥 Đề thi HOT:

CHỌN BỘ SÁCH BẠN MUỐN XEM

Đăng ký

Đăng nhập

Quên mật khẩu

b, Chứng minh MI² = MH.MK;

Cho nữa đường tròn tâm O đường kính AB , kẻ tiếp tuyến Bx và lấy hai điểm C và D thuộc nửa đường tròn. Các tia AC và AD cắt Bx lần lượt ở E, F ( F ở giữa B và E)

1. Chứng minh: $\hat{A B D} = \hat{D F B}$ .