Cho hình chữ nhật ABCD có O là giao điểm 2 đường chéo. Điểm M trên đoạn OB, lấy E đối xứng với A qua M; H là hình chiếu của điểm E trên BC, vẽ hình chữ nhật EHCF. Chứng minh M, H, F thẳng hàng.
Cho hình chữ nhật ABCD có O là giao điểm 2 đường chéo. Điểm M trên đoạn OB, lấy E đối xứng với A qua M; H là hình chiếu của điểm E trên BC, vẽ hình chữ nhật EHCF. Chứng minh M, H, F thẳng hàng.
Quảng cáo
Trả lời:
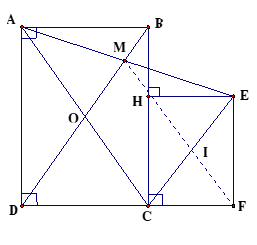
Gọi I là giao điểm của HF và CE.
H, I, F thẳng hàng (*) (t/c hình chữ nhật).
Cần chứng minh: M,I , F thẳng hàng.
(gt) và (t/c hình chữ nhật).
là đường trung bình của .
( 2 góc đồng vị).
Mà và (vì cân tại O, cân tại I , t/c hình chữ nhật).
mà (do IM là đường trung bình ).
M, I, Fthẳng hàng (tiên đề Ơclít).
Kết hợp (*)với ta có: M, H, F thẳng hàng.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
1)
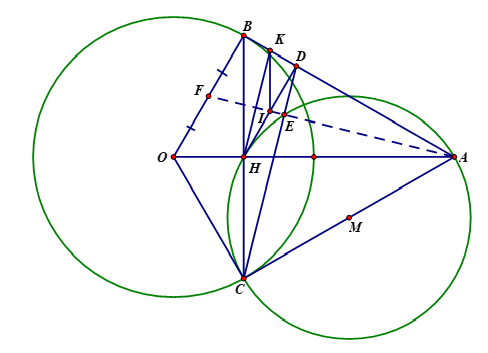
Ta có: (AB là tiếp tuyến của(O) tại B)
Þ DABO vuông tại B
Þ (Đ/L Pytago)
Þ Þ
Lời giải
2) Ta có DBOC cân tại O (OB = OC = R)
Mà OH là đường cao ( BC ^ OA tại H)
Þ OH là đường phân giác của DBOC
Þ
Chứng minh DAOC = DAOB (c-g-c)
Þ
Mà (AB là tiếp tuyến của(O) tại B)
Þ
Þ AC ^ OC
Þ Mà C thuộc (O)
Þ AC là tiếp tuyến của đường tròn (O)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.