Hai đường tròn (O;R) và (O';r) tiếp xúc ngoài tại gọi AC và BC là hai đường kính đi qua C của đường tròn (O) và (O'). DE là dây cung của đường tròn (O) vuông góc với AB tại trung điểm M của AB. Tia DC cắt đường tròn (O') tại điểm thứ 2 là F. Chứng minh MF là tiếp tuyến của (O')
Quảng cáo
Trả lời:
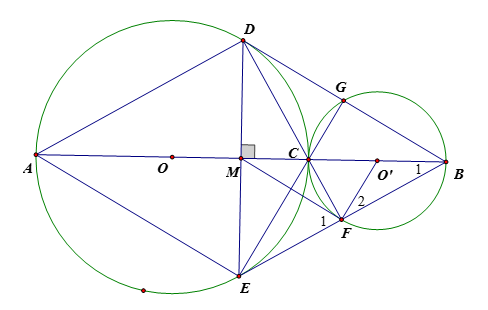
Nhận thấy và mà nên , suy ra . Vậy MF là tia tiếp tuyến của đường tròn tâm O’.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Ta có (nội tiếp chắn nửa đường tròn (O)) => .
Tứ giác AMEB có ; => mà đây là hai góc đối nên tứ giác AMEB nội tiếp một đường tròn =>
Tứ giác ABCD là tứ giác nội tiếp => ( nội tiếp cùng chắn cung CD)
=> => AM là tia phân giác của góc DAE (2)
Từ (1) và (2) ta có M là tâm đường tròn nội tiếp tam giác ADE.
Lời giải
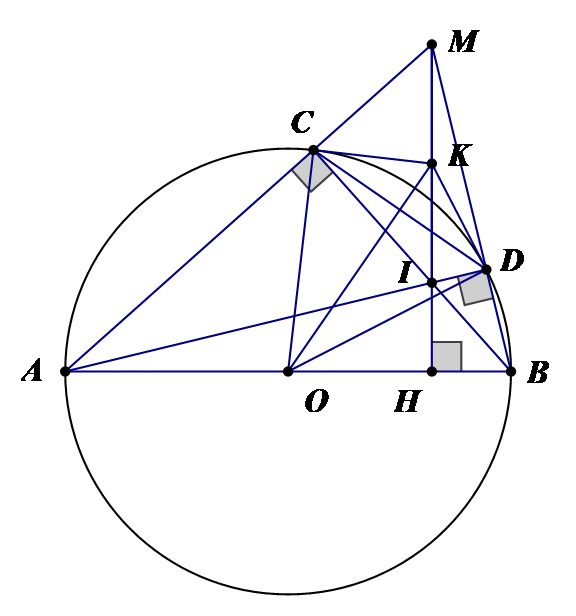
( nội tiếp chắn nửa đường tròn ) ….
=> mà đây là hai góc đối của tứ giác MCID nên MCID là tứ giác nội tiếp.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.