Câu hỏi:
12/07/2024 555
Có ba trạm quan sát A, B, C, trong đó trạm quan sát C ở giữa hồ. Người ta muốn đo khoảng cách từ A và từ B đến C. Do không thể đo trực tiếp được khoảng cách trên nên người ta làm như sau (Hình 42):
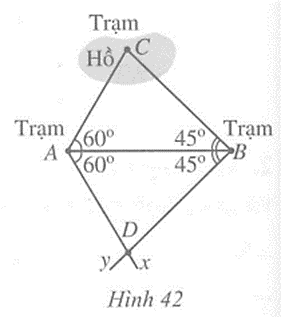
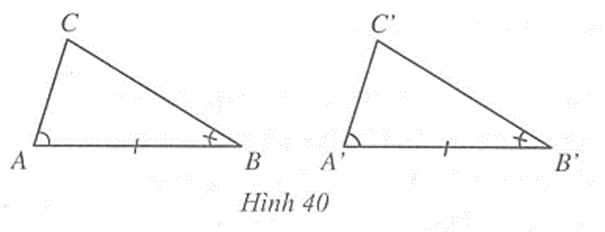
- Đo góc BAC được 60o, đo góc ABC được 45o.
- Kẻ tia Ax sao cho \(\widehat {{\rm{BAx}}}\) = 60o, kẻ tia By sao cho \(\widehat {ABy}\) = 45o, xác định giao điểm D của hai tia đó.
- Đo khoảng cách AD và BD. Ta có AC = AD và BC = BD.
Em hãy giải thích cách làm đó.
Có ba trạm quan sát A, B, C, trong đó trạm quan sát C ở giữa hồ. Người ta muốn đo khoảng cách từ A và từ B đến C. Do không thể đo trực tiếp được khoảng cách trên nên người ta làm như sau (Hình 42):
- Đo góc BAC được 60o, đo góc ABC được 45o.
- Kẻ tia Ax sao cho \(\widehat {{\rm{BAx}}}\) = 60o, kẻ tia By sao cho \(\widehat {ABy}\) = 45o, xác định giao điểm D của hai tia đó.
- Đo khoảng cách AD và BD. Ta có AC = AD và BC = BD.
Em hãy giải thích cách làm đó.
Quảng cáo
Trả lời:
Giải bởi Vietjack
Xét hai tam giác ABC và ABD, ta có:
\(\widehat {CAB}\) = \(\widehat {DAB}\)= 60o, \(\widehat {CBA}\) = \(\widehat {DBA}\)= 45o, AB là cạnh chung
Suy ra ∆ABC = ∆ABD (g.c.g).
Do đó AC = AD, BC = BD (hai cạnh tương ứng)
Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay
Sách thầy cô Vietjack biên soạn:
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
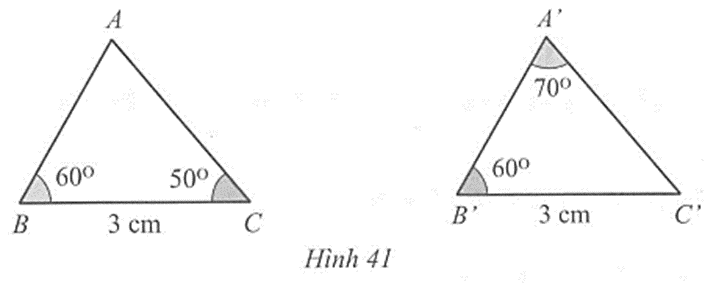
Xét tam giác A’B’C’, ta có: \(\widehat {A'}\) + \(\widehat {B'}\) + \(\widehat {C'}\) = 180o, (tổng ba góc của một tam giác)
Suy ra cm, \(\widehat {C'}\) = 180o – (\(\widehat {A'}\) + \(\widehat {B'}\)) = 180o – ( 70o + 60o) = 50o.
Xét hai tam giác ABC và A’B’C’ ta có:
BC = B’C’ = 3 cm, \(\widehat B\) = \(\widehat {B'}\) = 60o, \(\widehat C\) = \(\widehat {C'}\) = 50o,
Suy ra ∆ABC = ∆A’B’C’ (g.c.g).
Lời giải
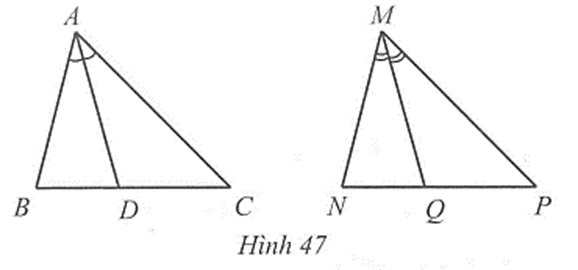
Vì AD là tia phân giác của góc BAC nên \(\widehat {BAD} = \frac{1}{2}\widehat {BAC}\);
MQ là tia phân giác của góc NMP nên \(\widehat {NMQ}\) = \[\frac{1}{2}\widehat {NMP}\];
Mà \(\widehat {BAC}\) = \(\widehat {NMP}\) (vì ∆ABC = ∆MNP), suy ra \(\widehat {BAD}\) = \(\widehat {NMQ}\)
Xét hai tam giác ABD và NMQ, ta có:
\(\widehat {BAD}\) = \(\widehat {NMQ}\), AB = MN, \(\widehat B\) = \(\widehat N\)(vì ∆ABC = ∆MNP).
Suy ra ∆ABD = ∆MNQ (g.c.g).
Do đó AD = MQ (hai cạnh tương ứng).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
Đề kiểm tra cuối học kỳ 2 Toán 7 Kết nối tri thức có đáp án - Đề 1
-
Đề kiểm tra cuối học kỳ 2 Toán 7 Kết nối tri thức có đáp án - Đề 2
-
Bộ 7 đề thi học kì 2 Toán lớp 7 Chân trời sáng tạo có đáp án - Đề 04
-
15 câu Trắc nghiệm Toán 7 Kết nối tri thức Bài 1: Tập hợp các số hữu tỉ có đáp án
-
Bộ 7 đề thi học kì 2 Toán 7 Cánh Diều có đáp án - Đề 01
-
Bộ 7 đề thi học kì 2 Toán lớp 7 Chân trời sáng tạo có đáp án - Đề 01
-
Đề kiểm tra cuối học kỳ 2 Toán 7 Kết nối tri thức có đáp án - Đề 3
-
Bộ 7 đề thi học kì 2 Toán 7 Cánh Diều có đáp án - Đề 02
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận