Giải VBT Toán 7 Cánh diều Bài 6. Trường hợp thứ ba của tam giác: góc - cạnh - góc có đáp án
41 người thi tuần này 4.6 2 K lượt thi 14 câu hỏi
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Bộ 10 đề thi cuối kì 2 Toán 7 Cánh diều có đáp án - Đề 10
Bộ 10 đề thi cuối kì 2 Toán 7 Cánh diều có đáp án - Đề 9
Bộ 10 đề thi cuối kì 2 Toán 7 Cánh diều có đáp án - Đề 8
Bộ 10 đề thi cuối kì 2 Toán 7 Cánh diều có đáp án - Đề 7
Bộ 10 đề thi cuối kì 2 Toán 7 Cánh diều có đáp án - Đề 6
Bộ 10 đề thi cuối kì 2 Toán 7 Cánh diều có đáp án - Đề 5
Bộ 10 đề thi cuối kì 2 Toán 7 Cánh diều có đáp án - Đề 4
Bộ 10 đề thi cuối kì 2 Toán 7 Cánh diều có đáp án - Đề 3
Danh sách câu hỏi:
Lời giải
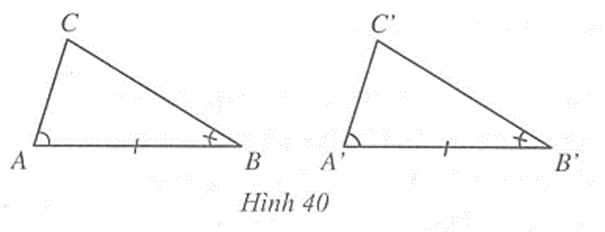
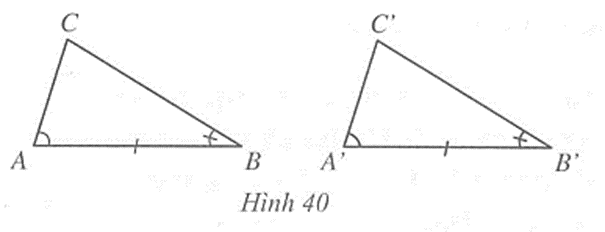
- Nếu một cạnh và hai góc kề nhau của tam giác này bằng một cạnh và hai góc kề nhau của tam giác kia thì hai tam giác đó bằng nhau.
Nếu \(\widehat A\) = \(\widehat {A'}\), AB = A’B’, \(\widehat B\) = \(\widehat {B'}\) thì ∆ABC = ∆A’B’C’ (g.c.g) (Hình 40).
Lời giải
- Nếu một cạnh góc vuông và góc nhọn kề cạnh ấy của tam giác vuông này bằng một cạnh góc vuông và góc nhọn kề cạnh ấy của tam giác vuông kia thì hai tam giác vuông đó bằng nhau.
- Nếu cạnh huyền và một góc nhọn của tam giác vuông này bằng cạnh huyền và một góc nhọn của tam giác vuông kia thì hai tam giác vuông đó bằng nhau.
Nhận xét
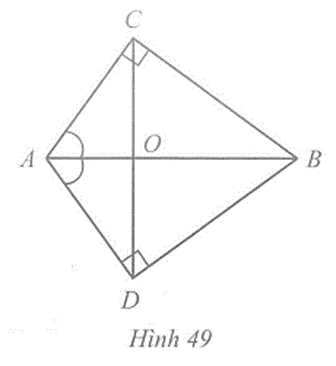
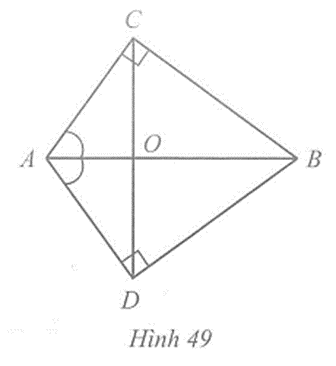
+ Nếu một điểm nằm trên tia phân giác của một góc thì cách đều hai cạnh của góc đó
+ Nếu một điểm nằm trong một góc và cách đều hai cạnh của góc thì nằm trên tia phân giác của góc đó.
Lời giải
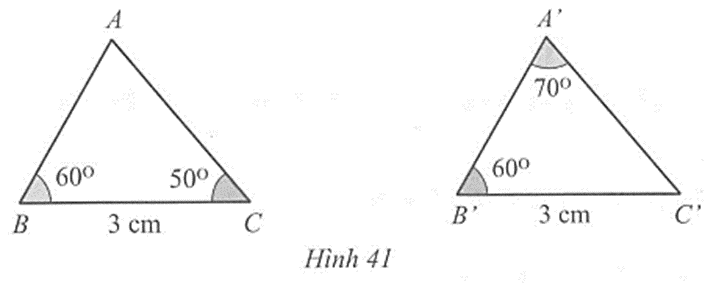
Xét tam giác A’B’C’, ta có: \(\widehat {A'}\) + \(\widehat {B'}\) + \(\widehat {C'}\) = 180o, (tổng ba góc của một tam giác)
Suy ra cm, \(\widehat {C'}\) = 180o – (\(\widehat {A'}\) + \(\widehat {B'}\)) = 180o – ( 70o + 60o) = 50o.
Xét hai tam giác ABC và A’B’C’ ta có:
BC = B’C’ = 3 cm, \(\widehat B\) = \(\widehat {B'}\) = 60o, \(\widehat C\) = \(\widehat {C'}\) = 50o,
Suy ra ∆ABC = ∆A’B’C’ (g.c.g).
Lời giải
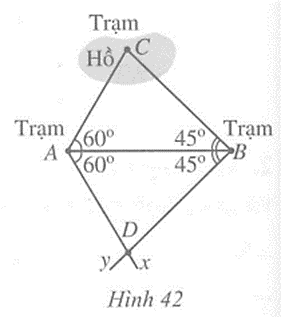
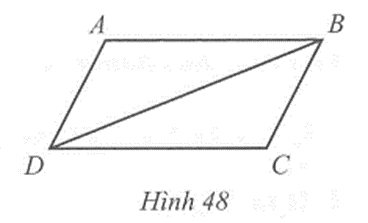
Xét hai tam giác ABC và ABD, ta có:
\(\widehat {CAB}\) = \(\widehat {DAB}\)= 60o, \(\widehat {CBA}\) = \(\widehat {DBA}\)= 45o, AB là cạnh chung
Suy ra ∆ABC = ∆ABD (g.c.g).
Do đó AC = AD, BC = BD (hai cạnh tương ứng)
Lời giải
Xét hai tam giác ABC và A’B’C’, ta có: , \(\widehat A\) + \(\widehat B\) + \(\widehat C\) = \(\widehat {A'}\) + \(\widehat {B'}\) + \(\widehat {C'}\) = 180o (tổng ba góc của một tam giác)
Mà \(\widehat A\) = \(\widehat {A'}\), \(\widehat C\) = \(\widehat {C'}\)(giả thiết) nên \(\widehat B\) = \(\widehat {B'}\)
Xét hai tam giác ABC và A’B’C’, ta có:
AB = A’B’ (giả thiết), \(\widehat A\) = \(\widehat {A'}\) và \(\widehat B\) = \(\widehat {B'}\)
Suy ra: ∆ABC = ∆A’B’C’ (g.c.g).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.