Câu hỏi:
11/07/2024 3,666
Cho hai điểm M, N lần lượt nằm trên các cạnh AB, AC của tam giác ABC sao cho \(\widehat {ABN} = \widehat {ACM}\). Gọi O là giao điểm của BN và CM. Chứng minh rằng:
a) AM . AB = AN . AC.
b) OM . OC = ON . OB.
Cho hai điểm M, N lần lượt nằm trên các cạnh AB, AC của tam giác ABC sao cho \(\widehat {ABN} = \widehat {ACM}\). Gọi O là giao điểm của BN và CM. Chứng minh rằng:
a) AM . AB = AN . AC.
b) OM . OC = ON . OB.
Quảng cáo
Trả lời:
Giải bởi Vietjack
Lời giải
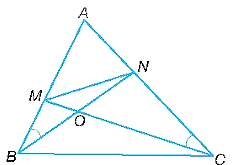
a)
Xét tam giác ABN và tam giác ACM có:
\(\widehat A\) chung
\(\widehat {ABN} = \widehat {ACM}\) (gt)
Do đó, ∆ABN ᔕ ∆ACM (g.g).
Suy ra \(\frac{{AB}}{{AC}} = \frac{{AN}}{{AM}}\) nên AM . AB = AN . AC.
b)
Tam giác BOM và tam giác CON có:
\(\widehat {MBO} = \widehat {NCO}\) (do \(\widehat {ABN} = \widehat {ACM}\))
\(\widehat {MOB} = \widehat {NOC}\) (hai góc đối đỉnh)
Nên ∆BOM ᔕ ∆CON (g.g).
Suy ra \(\frac{{OM}}{{ON}} = \frac{{OB}}{{OC}}\) nên OM . OC = ON . OB.
Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay
Sách thầy cô Vietjack biên soạn:
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Lời giải
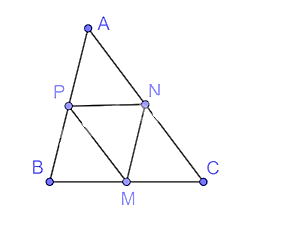
Tam giác ABC có:
M, N lần lượt là trung điểm của BC, CA
Nên MN là đường trung bình của tam giác ABC.
Do đó, MN // AB và \(\frac{{AB}}{{MN}} = 2\).
Chứng minh tương tự ta có: \(\frac{{BC}}{{PN}} = 2\); \(\frac{{AC}}{{PM}} = 2\).
Tam giác ABC và tam giác MNP có:
\(\frac{{AB}}{{MN}} = \frac{{BC}}{{PN}} = \frac{{AC}}{{PM}}\) (= 2).
Nên ∆ABC ᔕ ∆MNP (c.c.c) theo tỉ số đồng dạng là 2.
Lời giải
Lời giải
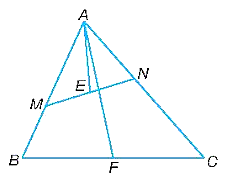
a)
Vì AM . AB = AN . AC nên \(\frac{{AM}}{{AC}} = \frac{{AN}}{{AB}}\).
Tam giác AMN và tam giác ABC có:
\(\frac{{AM}}{{AC}} = \frac{{AN}}{{AB}}\),
\(\widehat {BAC}\) chung.
Do đó, ∆AMN ᔕ ∆ACB (c.g.c).
b)
Vì ∆AMN ᔕ ∆ACB (cmt) nên \(\widehat {AMN} = \widehat C\) và \(\frac{{AM}}{{AC}} = \frac{{MN}}{{CB}}\).
Mà E, F lần lượt là trung điểm của MN, BC nên MN = 2ME, BC = 2FC.
Do đó: \(\frac{{AM}}{{AC}} = \frac{{MN}}{{CB}} = \frac{{2ME}}{{2FC}} = \frac{{ME}}{{FC}}\).
Tam giác MAE và tam giác CAF có:
\(\widehat {AME} = \widehat C\) (do \(\widehat {AMN} = \widehat C\));
\(\frac{{AM}}{{AC}} = \frac{{ME}}{{FC}}\) (cmt).
Do đó, ∆AME ᔕ ∆ACF (c.g.c). Suy ra \(\widehat {EAM} = \widehat {FAC}\) (hai góc tương ứng).
Vậy \(\widehat {EAB} = \widehat {FAC}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
Bộ 10 đề thi cuối kì 2 Toán 8 Kết nối tri thức cấu trúc mới có đáp án (Đề 1)
-
15 câu Trắc nghiệm Toán 8 Kết nối tri thức Bài 1: Đơn thức có đáp án
-
Dạng 1: Bài luyện tập 1 dạng 1: Tính có đáp án
-
Đề kiểm tra cuối kỳ 2 Toán 8 có đáp án ( Mới nhất)_ đề 24
-
Bộ 10 đề thi giữa kì 2 Toán 8 Kết nối tri thức cấu trúc mới có đáp án (Đề 1)
-
Đề kiểm tra cuối kỳ 2 Toán 8 có đáp án ( Mới nhất)_ đề 1
-
Đề cuối kì 2 Toán 8 Chân trời sáng tạo cấu trúc mới có đáp án - Đề 1
-
Bộ 10 đề thi cuối kì 2 Toán 8 Kết nối tri thức cấu trúc mới có đáp án (Đề 2)
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận