Giải SBT Toán 8 KNTT Bài 34. Ba trường hợp đồng dạng của hai tam giác có đáp án
73 người thi tuần này 4.6 685 lượt thi 19 câu hỏi
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Bộ 10 đề thi giữa kì 2 Toán 8 Chân trời sáng tạo có đáp án - Đề 10
Bộ 10 đề thi giữa kì 2 Toán 8 Chân trời sáng tạo có đáp án - Đề 09
Bộ 10 đề thi giữa kì 2 Toán 8 Chân trời sáng tạo có đáp án - Đề 08
Bộ 10 đề thi giữa kì 2 Toán 8 Chân trời sáng tạo có đáp án - Đề 07
Bộ 10 đề thi giữa kì 2 Toán 8 Chân trời sáng tạo có đáp án - Đề 06
Bộ 10 đề thi giữa kì 2 Toán 8 Chân trời sáng tạo có đáp án - Đề 05
Bộ 10 đề thi giữa kì 2 Toán 8 Chân trời sáng tạo có đáp án - Đề 04
Bộ 10 đề thi giữa kì 2 Toán 8 Chân trời sáng tạo có đáp án - Đề 03
Danh sách câu hỏi:
Lời giải
Lời giải
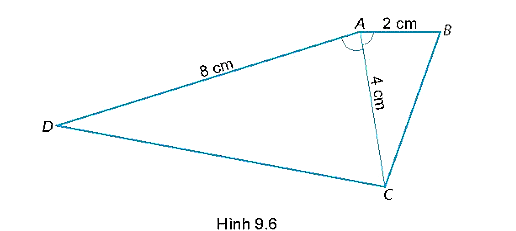
(1) Vì \(\frac{2}{6} = \frac{3}{9} = \frac{4}{{12}}\) nên hai tam giác này đồng dạng với nhau theo trường hợp cạnh – cạnh – cạnh.
(2) Vì \(\frac{3}{6} = \frac{5}{{10}} \ne \frac{6}{{11}}\) nên hai tam giác này không đồng dạng với nhau.
(3) Vì \(\frac{2}{2} = \frac{3}{3} \ne \frac{3}{2}\) nên hai tam giác này không đồng dạng với nhau.
(4) Vì \(\frac{4}{3} = \frac{4}{3} = \frac{4}{3}\) nên hai tam giác này đồng dạng với nhau theo trường hợp cạnh – cạnh – cạnh.
Lời giải
Lời giải
Theo tính chất dãy tỉ số bằng nhau ta có:
\(\frac{3}{4} = \frac{{AB}}{{DE}} = \frac{{AC}}{{DF}} = \frac{{AB + AC}}{{DE + DF}} = \frac{{15 - BC}}{{20 - FE}}\)
Do đó,
4(15 – BC) = 3(20 – FE)
60 – 4BC = 60 – 3FE
4BC = 3FE
Suy ra \(\frac{{BC}}{{FE}} = \frac{3}{4}\).
Tam giác ABC và tam giác DEF có:
\(\frac{{AB}}{{DE}} = \frac{{AC}}{{DF}} = \frac{{BC}}{{EF}}\left( { = \frac{3}{4}} \right)\).
Nên ∆ABC ᔕ ∆DEF (c.c.c).
Lời giải
Lời giải
Vì DE = 6 cm, DF = 4 cm, EF = 3 cm nên ta có: DE : DF : EF = 6 : 4 : 3.
Do đó \(\frac{{DE}}{6} = \frac{{DF}}{4} = \frac{{EF}}{3}\). Suy ra \(\frac{{2DE}}{{12}} = \frac{{3DF}}{{12}} = \frac{{4EF}}{{12}}\).
Suy ra 2DE = 3DF = 4EF.
Mà 2AB = 3AC = 4BC (gt)
Do đó, \(\frac{{AB}}{{DE}} = \frac{{AC}}{{DF}} = \frac{{BC}}{{EF}}\).
Suy ra, ∆ABC ᔕ ∆DEF (c.c.c).
Lời giải
Lời giải
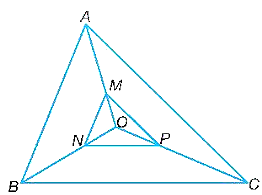
Vì OA = 3OM, OB = 3ON, OC = 3OP.
Nên \(\frac{{OA}}{{OM}} = 3;\frac{{OB}}{{ON}} = 3;\frac{{OC}}{{OP}} = 3\). Suy ra \(\frac{{OA}}{{OM}} = \frac{{OB}}{{ON}} = \frac{{OC}}{{OP}} = 3\).
Tam giác OMN có: \(\frac{{OA}}{{OM}} = \frac{{OB}}{{ON}}\).
Nên suy ra AB song song với MN (định lí Thalès đảo).
Do đó, \(\frac{{AB}}{{MN}} = \frac{{OA}}{{OM}} = 3\).
Chứng minh tương tự ta có: \(\frac{{AC}}{{MP}} = 3;\frac{{BC}}{{NP}} = 3\).
Tam giác ABC và tam giác MNP có:
\(\frac{{AB}}{{MN}} = \frac{{AC}}{{MP}} = \frac{{BC}}{{NP}} = 3\).
Do đó, ∆ABC ᔕ ∆MNP (c.c.c) với tỉ số đồng dạng 3.
Lời giải
Lời giải
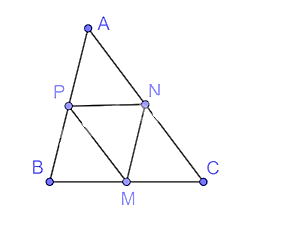
Tam giác ABC có:
M, N lần lượt là trung điểm của BC, CA
Nên MN là đường trung bình của tam giác ABC.
Do đó, MN // AB và \(\frac{{AB}}{{MN}} = 2\).
Chứng minh tương tự ta có: \(\frac{{BC}}{{PN}} = 2\); \(\frac{{AC}}{{PM}} = 2\).
Tam giác ABC và tam giác MNP có:
\(\frac{{AB}}{{MN}} = \frac{{BC}}{{PN}} = \frac{{AC}}{{PM}}\) (= 2).
Nên ∆ABC ᔕ ∆MNP (c.c.c) theo tỉ số đồng dạng là 2.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.