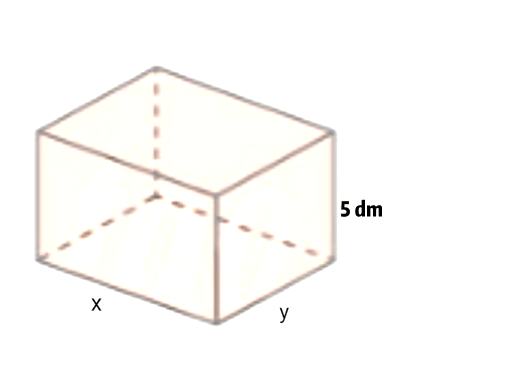
Để thiết kế một bể cá không nắp có dạng hình hộp chữ nhật có chiều cao là 80 cm, thể tích là 12800 cm3. Người thợ dùng loại kính để sử dụng làm mặt bên có giá thành 70000 VNĐ/m2 và loại kính để làm mặ...

Câu hỏi:

19/03/2025 427

Để thiết kế một bể cá không nắp có dạng hình hộp chữ nhật có chiều cao là 80 cm, thể tích là 12800 cm³. Người thợ dùng loại kính để sử dụng làm mặt bên có giá thành 70000 VNĐ/m² và loại kính để làm mặt đáy có giá thành 100000 VNĐ/m². Gọi x là chiều dài của đáy bể cá với (x > 0, x (m)); f(x) là hàm số xác định chi phí để hoàn thành bể cá. Đồ thị hàm số f(x) có bao nhiêu đường tiệm cận?

A. 1;

B. 2;

C. 3;

D. 4.

Xem lời giải

Câu hỏi trong đề: 12 bài tập Một số bài toán thực tế ứng dụng đường tiệm cận của đồ thị hàm số có lời giải !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

Đáp án đúng là: B

Gọi y là chiều rộng của đáy bể cá (y > 0, m).

Ta có :\[0,8xy = 0,0128 \Rightarrow y = \frac{{0,016}}{x}\left( m \right)\].

Giá thành bể cá được xác định theo hàm số:

\[f\left( x \right) = 2.0,8\left( {x + \frac{{0,016}}{x}} \right).70000 + 100000.x.\frac{{0,016}}{x}\] (VNĐ)

\[ \Rightarrow f\left( x \right) = 112000\left( {x + \frac{{0,016}}{x}} \right) + 1600\](VNĐ)

\[ \Rightarrow f\left( x \right) = 112000x + 1600 + \frac{{1792}}{x}\](VNĐ).

Ta có:\[\mathop {\lim }\limits_{x \to {0^ + }} f\left( x \right) = \mathop {\lim }\limits_{x \to {0^ + }} \left( {112000x + 1600 + \frac{{1792}}{x}} \right) = + \infty \].

\[\mathop {\lim }\limits_{x \to + \infty } \left[ {f\left( x \right) - (112000x + 1600)} \right] = \mathop {\lim }\limits_{x \to + \infty } \frac{{1792}}{x} = 0\].

Nên đồ thị hàm f(x) có tiệm cận đứng là x = 0; tiệm cận xiên là y = 112000x + 1600.

Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

Bình luận

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Số dân của một thị trấn sau t năm kể từ năm 1970 được ước tính bởi công thức \(f\left( t \right) = \frac{{26t + 10}}{{t + 5}}\); f(t) được tính bằng nghìn người. Xem f(t) là một hàm số xác định trên nửa khoảng [0; +∞). Đồ thị hàm số y = f(t) có đường tiệm cận ngang y = a. Giá trị của a là bao nhiêu?

A. 20;

B. 36;

C. 10;

D. 26.

Lời giải

Đáp án đúng là: D

Ta có \(\mathop {\lim }\limits_{t \to \infty } f\left( t \right) = \mathop {\lim }\limits_{t \to \infty } \frac{{26t + 10}}{{t + 5}} = 26\). Nên đồ thị hàm số f(t) có đường tiệm cận ngang là y = 26.

Câu 2

Người ta muốn làm một cái bể dạng hình hộp chữ nhật không nắp (như hình vẽ) có thể tích bằng 1 m³. Chiều cao của bể là 5 dm, các kích thước khác là x (m), y (m) với x > 0 và y > 0. Diện tích toàn phần của bể (không kể nắp) là hàm số S(x) trên khoảng (0; +∞). Đường tiệm cận xiên của đồ thị hàm số S(x) là đường thẳng y = ax + b. Tính giá trị của biểu thức P = a² + b² .

B. 2;

C. 3;

D. 4.

Lời giải

Đáp án đúng là: A

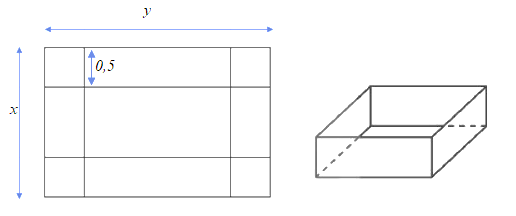
Do thể tích của bể là 1 m³ nên 0,5xy = 1 xy = 2 .

Diện tích toàn phần của bể là \(S\left( x \right) = xy + 2.0,5.x + 2.0,5.y = 2 + x + \frac{2}{x},\,\,\,\,\left( {x > 0} \right)\).

Ta có: \(\mathop {\lim }\limits_{x \to + \infty } \left( {S\left( x \right) - \left( {x + 2} \right)} \right) = \mathop {\lim }\limits_{x \to + \infty } \frac{2}{x} = 0\).

Suy ra đồ thị hàm số S(x) có đường tiệm cận xiên là y = x + 2 a = 1; b = 2.

Vậy P = a² + b² = 5.

Câu 3