Một công ty sản xuất đồ gia dụng ước tính chi phí để sản xuất x (sản phẩm) là C(x)=2x+50 (triệu đồng). Khi đó \[f(x) = \frac{{C(x)}}{x}\] là chi phí sản xuất trung bình cho mỗi sản phẩm. Chứng tỏ rằng hàm số f(x) giảm và \[\mathop {\lim }\limits_{x \to + \infty } f(x) = 2\]. Tính chất này nói lên điều gì?
Quảng cáo
Trả lời:
Giải bởi Vietjack
Ta có: \(f(x) = \frac{{C(x)}}{x} = \frac{{2x + 50}}{x}\)
Vì \({f^\prime }(x) = \frac{{ - 50}}{{{x^2}}} < 0\) với mọi số thực \({\rm{x}}\) nên hàm số \(f(x) = \frac{{C(x)}}{x}\) giảm.
\(\mathop {\lim }\limits_{x \to + \infty } f(x) = \mathop {\lim }\limits_{x \to + \infty } \frac{{2x + 50}}{x} = \mathop {\lim }\limits_{x \to + \infty } \frac{{2 + \frac{{50}}{x}}}{1} = 2{\rm{ (dpcm) }}\)
Tính chất này nói lên: Khi sản xuất càng nhiều sản phầm thì chi phí sản xuất trung bình cho mỗi sản phẩm càng giảm, nhưng không dưới 2 .
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
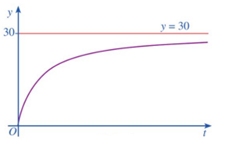
a) Sau 1 phút, ta có: khối lượng muối trong bể là 25 . 30 . t = 750t (gam); thể tích của lượng nước trong bể là 5 000 + 25t (lít). Vậy nồng độ muối sau 1 phút là \[f(t) = \frac{{750t}}{{5000 + 25t}} = \frac{{30t}}{{200 + t}}\] (gam/lít).
b) Ta có: \[\mathop {\lim }\limits_{t \to + \infty } f(t) = \mathop {\lim }\limits_{t \to + \infty } \frac{{30t}}{{200 + t}} = \mathop {\lim }\limits_{t \to + \infty } \left( {30 - \frac{{6000}}{{200 + t}}} \right) = 30\]
Vậy đường thẳng y = 30 là tiệm cận ngang của đồ thị hàm số f(t).
c) Ta có đồ thị hàm số y = f(t) nhận đường thẳng y = 30 làm tiệm cận ngang, tức là khi t càng lớn thì nồng độ muối trong bể sẽ tiến gần đến mức 30 (gam/lít). Lúc đó, nồng độ muối trong bể sẽ gần như bằng nồng độ muối trong nước muối được bơm vào bể.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
a) Xét hàm số \(y = S(x) = 200\left( {5 - \frac{9}{{2 + x}}} \right)\) với \(x \in [1; + \infty )\).
Ta có \(\mathop {\lim }\limits_{x \to + \infty } y = \mathop {\lim }\limits_{x \to + \infty } 200\left( {5 - \frac{9}{{2 + x}}} \right) = 1000;\mathop {\lim }\limits_{x \to - \infty } = 200\left( {5 - \frac{9}{{2 + x}}} \right) = 1000\).
Do đó, đường thẳng \(y = 1000\) là tiệm cận ngang của đồ thị hàm số đã cho trên nửa khoảng \([1; + \infty )\).
b) Ta có đồ thị hàm số \(y = S(x)\) với \(x \in [1; + \infty )\) nhận đường thẳng \(y = 1000\) làm tiệm cận ngang, tức là khi \(x\) càng lớn thì số lượng sản phấm bán được của công ty đó trong \({\rm{x}}\) (tháng) sẽ tiến gần đến 1000 sản phấm.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập