Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như hình bên dưới. Hỏi đồ thị hàm số đã cho có tất cả bao nhiêu đường tiệm cận đứng và ngang?
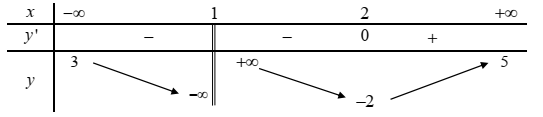
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như hình bên dưới. Hỏi đồ thị hàm số đã cho có tất cả bao nhiêu đường tiệm cận đứng và ngang?

Quảng cáo
Trả lời:
Ta có
\(\mathop {\lim }\limits_{x \to - \infty } y = 3\)nên \(y = 3\) là tiệm cận ngang của đồ thị hàm số.
\(\mathop {\lim }\limits_{x \to + \infty } y = 5\)nên \(y = 5\) là tiệm cận ngang của đồ thị hàm số.
\(\left\{ {\begin{array}{*{20}{c}}{\mathop {\lim }\limits_{x \to {1^ - }} y = - \infty }\\{\mathop {\lim }\limits_{x \to {1^ + }} y = + \infty }\end{array}} \right.\)nên \(x = 1\) là tiệm cận đứng của đồ thị hàm số.
Vậy đồ thị hàm số đã cho có \(3\) tiệm cận đứng và ngang.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Tập xác định: \[D = \mathbb{R}\backslash \left\{ { - 1} \right\}\].
Vì \[\mathop {\lim }\limits_{x \to {{\left( { - 1} \right)}^ + }} y = - \infty \]\[ \Rightarrow \] \[{\Delta _1}:x = - 1\] là tiệm cận đứng của \[\left( C \right)\].
\[\mathop {\lim }\limits_{x \to \pm \infty } y = 2\]\[ \Rightarrow \]\[{\Delta _2}:y = 2\]là tiệm cận ngang của \[\left( C \right)\].
Ta có \[y = \frac{{2x - 1}}{{x + 1}} = 2 - \frac{3}{{x + 1}}\], gọi \[M\left( {a;2 - \frac{3}{{a + 1}}} \right) \in \left( C \right)\], \[\left( {a \ne - 1} \right)\].
\[d\left( {M,{\Delta _1}} \right) = \left| {a + 1} \right|\].
\[d\left( {M,{\Delta _2}} \right) = \left| {\frac{{ - 3}}{{a + 1}}} \right| = \frac{3}{{\left| {a + 1} \right|}}\].
\[S = d\left( {M,{\Delta _1}} \right) + d\left( {M,{\Delta _2}} \right) = \left| {a + 1} \right| + \frac{3}{{\left| {a + 1} \right|}} \ge 2.\sqrt {\left| {a + 1} \right|.\frac{3}{{\left| {a + 1} \right|}}} = 2\sqrt 3 ,\forall a \ne - 1\].
Suy ra \[\min S = 2\sqrt 3 \], đạt được khi \[\left| {a + 1} \right| = \frac{3}{{\left| {a + 1} \right|}} \Leftrightarrow {\left( {a + 1} \right)^2} = 3\]\[ \Leftrightarrow \left[ \begin{array}{l}a = - 1 - \sqrt 3 \\a = - 1 + \sqrt 3 \end{array} \right.\].
Do đó \[{M_1}\left( { - 1 - \sqrt 3 ;2 + \sqrt 3 } \right)\], \[{M_2}\left( { - 1 + \sqrt 3 ;2 - \sqrt 3 } \right)\] là hai điểm trên \[\left( C \right)\] có tổng khoảng cách đến hai tiệm cận nhỏ nhất.
Vậy \[P = {x_1}.{x_2} + {y_1}.{y_2} = \left( { - 1 - \sqrt 3 } \right)\left( { - 1 + \sqrt 3 } \right) + \left( {2 + \sqrt 3 } \right)\left( {2 - \sqrt 3 } \right) = - 1\].
Lời giải
Đồ thị hàm số \[y = \frac{{2x + 1}}{{x - 3}}\] có các đường tiệm cận là \[x = 3,y = 2\].
Do vậy hai đường tiệm cận tạo với hai trục tọa độ hình chữ nhật diện tích bằng \[6\].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.