Câu hỏi:

13/08/2025 162

Tìm tất cả các giá trị của tham số \[m\] để hàm số \[f(x) = {x^3} + 3{x^2} + {m^2} - 5\] có giá trị lớn nhất trên đoạn \[\left[ { - 1\,;\,2} \right]\] là 19.
Trả lời: \[m = 2\] và \[m = - 2\].

Xem lời giải

Câu hỏi trong đề: (Trả lời ngắn) 32 bài tập GTLN, GTNN của hàm số (có lời giải) !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

Ta có \[f(x) = {x^3} + 3{x^2} + {m^2} - 5\].

\[f'(x) = 3{x^2} + 6x\]. \[f'(x) = 0 \Leftrightarrow 3{x^2} + 6x = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = - 2\end{array} \right.\].

Ta có: $f\left( 0 \right) = {m^2} - 5$, $f\left( { - 1} \right) = {m^2} - 3$, $f\left( 2 \right) = {m^2} + 15$

Do $f\left( x \right)$ liên tục trên đoạn \[\left[ { - 1\,;\,2} \right]\] khi đó:

$\mathop {\max }\limits_{x \in \left[ { - 1;2} \right]} f\left( x \right) = \max \left\{ {f\left( 0 \right),f\left( { - 1} \right),f\left( 2 \right)} \right\} = f\left( 2 \right) = {m^2} + 15$

Suy ra \[f(x)\] đạt GTLN tại \[x = 2\].

Khi đó \[{m^2} + 15 = 19 \Leftrightarrow {m^2} = 4 \Leftrightarrow \left[ \begin{array}{l}m = 2\\m = - 2\end{array} \right.\].

Hot: 1000+ Đề thi giữa kì 1 file word cấu trúc mới 2025 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Tìm giá trị lớn nhất, giá trị nhỏ nhất của các hàm số sau:
a) $y = x^{3} - 12 x + 1$ trên đoạn [-1;3]
b) $y = - x^{3} + 24 x^{2} - 180 x + 400$ trên đoạn [3;11]
c) $y = \frac{2 x + 1}{x - 2}$ trên đoạn $[3; 7]$
d) $y = \sin 2 x$ trên đoạn $[0; \frac{7 π}{12}]$

Trả lời:

a) $m a x_{[- 1; 3]} y = y (- 1) = 12$ và $m i n_{[- 1; 3]} y = y (2) = - 15$
b) $m a x_{[3; 11]} y = y (3) = 49$ và $m i n_{[3; 11]} y = y (6) = - 32$
c) $m a x_{[3; 7]} y = y (3) = 7$ và $m i n_{[3; 7]} y = y (7) = 3$
d) $m a x_{[0; \frac{7 π}{12}]} y = y (\frac{π}{4}) = 1$ và $m i n_{[0; \frac{7 π}{12}]} y = y (\frac{7 π}{12}) = - \frac{1}{2}$

Xem đáp án

Lời giải

a) Xét $y = x^{3} - 12 x + 1$ trên đoạn [-1;3]

$y' = 3 x^{2} - 12 = 0 \Leftrightarrow \{\begin{cases} x = 2 \\ x = - 2 (l o a i) \end{cases}$

Bảng biến thiên:

(Trả lời ngắn) Tìm giá trị lớn nhất, giá trị nhỏ nhất của các hàm số sau: a) y=x^3-12x+1 trên đoạn [-1;3] b) y=-x^3+24x^2-180x+400 trên đoạn [3;11] c) y=(2x+1)/(x-2) trên đoạn [3;7] d) y=sin⁡2x trên đoạn [0;7π/12] Trả lời: a) max_([-1;3]) y=y(-1)=12 và min_([-1;3]) y=y(2)=-15 b) max_([3;11]) y=y(3)=49 và min_([3;11]) y=y(6)=-32 c) max_([3;7]) y=y(3)=7 và min_([3;7]) y=y(7)=3 d) max_[0;7π/12] y=y(π/4)=1 và min_[0;7π/12] y=y(7π/12)=-1/2 (ảnh 1)

Từ bảng biến thiên, ta thấy $m a x_{[- 1; 3]} y = y (2) = - 15$ và
b) Xét $y = - x^{3}_24 x^{2} - 180 x + 400$ trên đoạn [3;11]

$y' = - 3 x^{2} + 48 x - 180 = 0 \Leftrightarrow \{\begin{cases} x = 10 \\ x = 6 \end{cases}$

Bảng biến thiên:

Từ bảng biến thiên, ta thấy $m a x_{[3; 11]} y = y (3) = 49$ và $m i n_{[3; 11]} y = y (6) = - 32$
c) Xét $y = \frac{2 x + 1}{x - 2}$ trên đoạn [3;7]

$y' = \frac{- 5}{{(x - 2)}^{2}} < 0 \forall x \in [3; 7]$

Bảng biến thiên:

Từ bảng biến thiên, ta thấy $m a x_{[3; 7]} y = y (3) = 7$ và $m i n_{[3; 7]} y = y (7) = 3$
d) Xét $y = \sin 2 x$ trên đoạn $[0; \frac{7 π}{12}]$

$y' = 2 \cos s 2 x = 0 \Leftrightarrow 2 x = \frac{π}{2} + k π \Leftrightarrow x = \frac{π}{4} + \frac{k π}{2} (k \in ℤ)$

Ta có: $x \in [0; \frac{7 π}{12}] \Rightarrow k = 0 \Rightarrow x = \frac{π}{4}$
Bảng biến thiên:

Từ bảng biến thiên, ta thấy $m a x_{[0; \frac{7 π}{12}]} y = (\frac{π}{4}) = 1$ và $m i n_{[0; \frac{7 π}{12}]} = y (\frac{7 π}{12}) = - \frac{1}{2}$

Câu 2

Người ta giăng lưới để nuôi riêng một loại cá trên một góc hồ. Biết rằng lưới được giăng theo một đường thẳng từ một vị trí trên bờ ngang đến một vị trí trên bờ dọc và phải đi qua một cái cọc đã cắm sẵn ở vị trí $A$. Hỏi diện tích nhỏ nhất có thể giăng là bao nhiêu, biết rằng khoảng cách từ cọc đến bờ ngang là $5\,m$ và khoảng cách từ cọc đến bờ dọc là $12\,m$.

$(Trả lời ngắn) Câu 31. Người ta giăng lưới để nuôi riêng một loại cá trên một góc hồ. Biết rằng lưới được giăng theo một đường thẳng từ một vị trí trên bờ ngang đến một vị trí trên bờ dọc và phải đi qua một cái cọc đã cắm sẵn ở vị trí $A$. Hỏi diện tích nhỏ nhất có thể giăng là bao nhiêu, biết rằng khoảng cách từ cọc đến bờ ngang là $5\,m$ và khoảng cách từ cọc đến bờ dọc là $12\,m$. Trả lời: $120{m^2}$. (ảnh 1)$
Trả lời: $120{m^2}$.

Xem đáp án

Lời giải

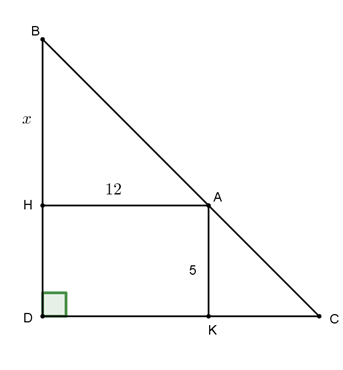
$(Trả lời ngắn) Câu 31. Người ta giăng lưới để nuôi riêng một loại cá trên một góc hồ. Biết rằng lưới được giăng theo một đường thẳng từ một vị trí trên bờ ngang đến một vị trí trên bờ dọc và phải đi qua một cái cọc đã cắm sẵn ở vị trí $A$. Hỏi diện tích nhỏ nhất có thể giăng là bao nhiêu, biết rằng khoảng cách từ cọc đến bờ ngang là $5\,m$ và khoảng cách từ cọc đến bờ dọc là $12\,m$. Trả lời: $120{m^2}$. (ảnh 2)$

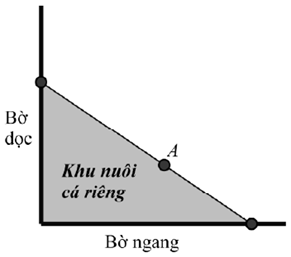
Gọi $H,\,K$ là hình chiếu của $A$ trên bờ dọc và bờ ngang. Đặt $BH = x\left( {x > 0} \right)$.

Khi đó, $\frac{{BH}}{{HD}} = \frac{{BA}}{{AC}} = \frac{{DK}}{{KC}} \Rightarrow KC = \frac{{HD.\,DK}}{{BH}} = \frac{{60}}{x}$.

Diện tích khu nuôi cá là:

$S = \frac{1}{2}BD.\,DC = \frac{1}{2}\left( {x + 5} \right)\left( {\frac{{60}}{x} + 12} \right) = 6x + \frac{{150}}{x} + 60 \ge 2\sqrt {6x.\frac{{150}}{x}} + 60$

$ \Rightarrow S \ge 120,\,S = 120\,\,khi\,\,x = 5$. Vậy diện tích nhỏ nhất có thể giăng là $120{m^2}$.

Câu 3