Một vật chuyển động theo quy luật \[s\left( t \right) = {t^3} - 3{t^2} - 9t + 2\]. Hỏi tại thời điểm nào thì vận tốc của vật đạt giá trị nhỏ nhất?
Một vật chuyển động theo quy luật \[s\left( t \right) = {t^3} - 3{t^2} - 9t + 2\]. Hỏi tại thời điểm nào thì vận tốc của vật đạt giá trị nhỏ nhất?
Quảng cáo
Trả lời:
Đáp án: 1
Ta có \[v\left( t \right) = {\left[ {s\left( t \right)} \right]^\prime } = 3{t^2} - 6t - 9\]
Cách 1: Phương trình \[v\left( t \right) = 3{t^2} - 6t - 9\]là một Parabol có đỉnh thấp nhất \[I\left\{ \begin{array}{l}{x_I} = \frac{{ - b}}{{2a}} = 1\\{y_I} = v\left( 1 \right) = - 12\end{array} \right.\].
Vậy vận tốc đạt giá trị nhỏ nhất khi \[{t_{\min }} = {x_I} = 1\].
Cách 2: Nhập phương trình bậc hai vào máy tính 580VNX, ta được:
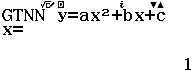
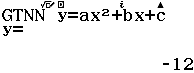
Vậy \[\left\{ \begin{array}{l}v\left( t \right) = {y_{\min }} = - 12\\{t_{\min }} = {x_{\min }} = 1\end{array} \right.\].
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đáp án: 1005
Xét hàm số \[N\left( t \right) = 1000 + \frac{{100t}}{{100 + {t^2}}},\,\left( {t > 0} \right)\]
\[N'\left( t \right) = \frac{{100\left( {100 + {t^2}} \right) - 2t.100t}}{{{{\left( {100 + {t^2}} \right)}^2}}} = \frac{{100\left( {100 - {t^2}} \right)}}{{{{\left( {100 + {t^2}} \right)}^2}}}\]
\[N'\left( t \right) = 0 \Leftrightarrow 100 - {t^2} = 0 \Leftrightarrow \left[ \begin{array}{l}t = 10\,\,\left( N \right)\\t = - 10\,\left( L \right)\end{array} \right.\].
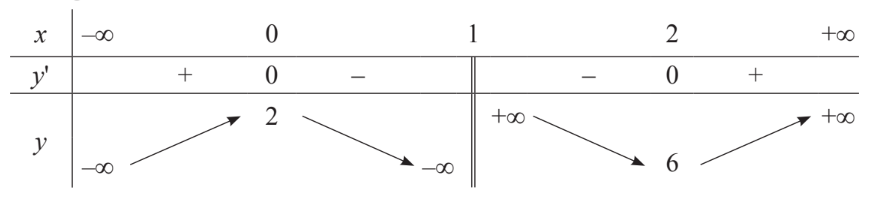
Ta có bảng biến thiên
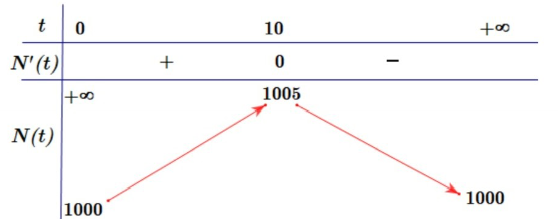
Vậy số lượng vi khuẩn lớn nhất nuôi cấy được là 1005 con.
Câu 2
Lời giải
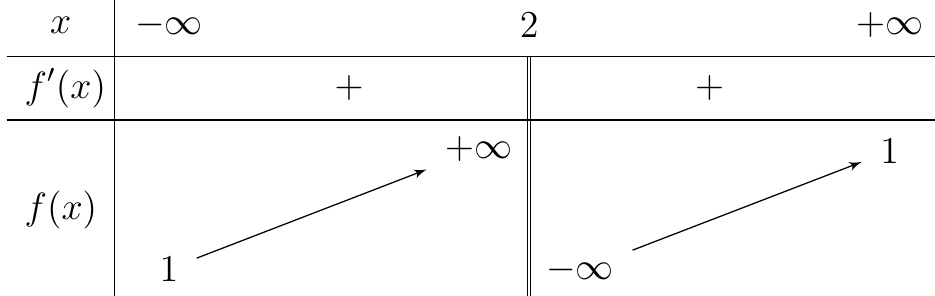
Dựa vào bảng biến thiên ta thấy đồ thị hàm số có tiệm cận đứng là đường thẳng \(x = 1\). Suy ra loại B và D.
Ta thấy đồ thị hàm số đi qua điểm \(\left( {0;2} \right)\) nên loại C.
Vậy bảng biến thiên đề bài cho là của hàm số \(y = \frac{{{x^2} + 2x - 2}}{{x - 1}}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.