Tại một cơ sở sản xuất nước tinh khiết, nhân viên phụ trách sản xuất cho biết, nếu mỗi ngày cơ sở này sản xuất \(x\,\,\left( {{{\rm{m}}^{\rm{3}}}} \right)\) nước tinh khiết thì phải chi phí các khoản sau: 5 triệu đồng chi phí cố định; \(0,15\) triệu đồng cho mỗi mét khối sản phẩm; \(0,0005{x^2}\)chi phí bảo dưỡng máy móc. Biết công suất tối đa mỗi ngày của cơ sở này là \(200\,{{\rm{m}}^{\rm{3}}}\). Gọi \(C\left( x \right)\) là chi phí sản xuất \(x\,\,\left( {{{\rm{m}}^{\rm{3}}}} \right)\) sản phẩm mỗi ngày và \(\overline c \left( x \right)\) là chi phí trung bình mỗi mét khối sản phẩm.
a) \(C\left( x \right) = 0,0005{x^2} + 0,15x + 5\).
b) Chi phí sản xuất \(100\,{{\rm{m}}^{\rm{3}}}\) nước tinh khiết là 20 triệu đồng.
c) \(\overline c \left( x \right) = 0,0005x + 0,15 + \frac{5}{x}\).
d) Chi phí trung bình giảm xuống khi sản lượng nước tính khiết trong ngày không vượt quá 100 \({{\rm{m}}^3}\).
Tại một cơ sở sản xuất nước tinh khiết, nhân viên phụ trách sản xuất cho biết, nếu mỗi ngày cơ sở này sản xuất \(x\,\,\left( {{{\rm{m}}^{\rm{3}}}} \right)\) nước tinh khiết thì phải chi phí các khoản sau: 5 triệu đồng chi phí cố định; \(0,15\) triệu đồng cho mỗi mét khối sản phẩm; \(0,0005{x^2}\)chi phí bảo dưỡng máy móc. Biết công suất tối đa mỗi ngày của cơ sở này là \(200\,{{\rm{m}}^{\rm{3}}}\). Gọi \(C\left( x \right)\) là chi phí sản xuất \(x\,\,\left( {{{\rm{m}}^{\rm{3}}}} \right)\) sản phẩm mỗi ngày và \(\overline c \left( x \right)\) là chi phí trung bình mỗi mét khối sản phẩm.
a) \(C\left( x \right) = 0,0005{x^2} + 0,15x + 5\).
b) Chi phí sản xuất \(100\,{{\rm{m}}^{\rm{3}}}\) nước tinh khiết là 20 triệu đồng.
c) \(\overline c \left( x \right) = 0,0005x + 0,15 + \frac{5}{x}\).
d) Chi phí trung bình giảm xuống khi sản lượng nước tính khiết trong ngày không vượt quá 100 \({{\rm{m}}^3}\).
Quảng cáo
Trả lời:
a) Đúng. Chi phí mỗi ngày là tổng các chi phí nên \(C\left( x \right) = 0,0005{x^2} + 0,15x + 5\) (triệu đồng).
b) Sai. Khi \(x = 100\), ta có \(C\left( {100} \right) = 0,0005 \times {100^2} + 0,15 \times 100 + 5 = 25\).
c) Sai. Chi phí trung bình trên mỗi khối sản phẩm là:
\(\overline c \left( x \right) = \frac{{0,0005{x^2} + 0,15x + 5}}{x} = 0,0005x + 0,15 + \frac{5}{x}\).
d) Đúng. Xét hàm số \(\overline c \left( x \right) = 0,0005x + 0,15 + \frac{5}{x}\), \(0 < x \le 200\).
Ta có \({\overline c ^{\,\prime }}\left( x \right) = \frac{5}{{{{10}^4}}} - \frac{5}{{{x^2}}}\), \({\overline c ^\prime }\left( x \right) = 0 \Leftrightarrow {x^2} = {10^4} \Rightarrow x = 100\) (do \(x \in \left( {0;200} \right]\).
Bảng biến thiên:
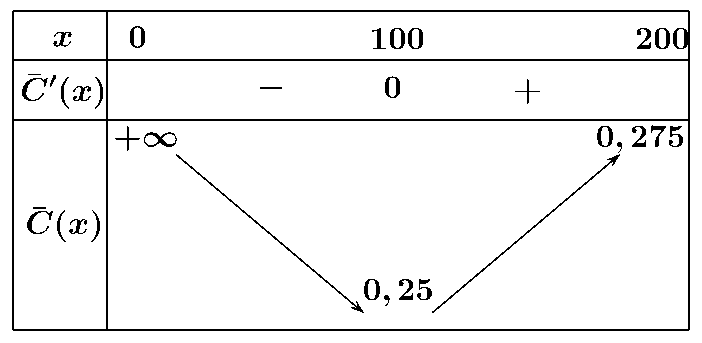
Vậy chi phí trung bình giảm khi hàm số \(\overline c \left( x \right)\)nghịch biến, tức là \(x \in \left( {0;100} \right)\).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
a) Đúng. Bán kính của hình bán nguyệt là \(\frac{x}{2}\) nên nửa chu vi bán nguyệt là \(\frac{{\pi x}}{2}\).
b) Đúng. Ta có \(2\left( {x + y} \right) + \frac{{\pi x}}{2} = 8 \Leftrightarrow y = 4 - \frac{{x\left( {4 + \pi } \right)}}{4}\).
c) Sai. Diện tích của cửa sổ:\(S = xy + \frac{1}{2}\pi {\left( {\frac{x}{2}} \right)^2} = x\left( {4 - x - \frac{{\pi x}}{4}} \right) + \frac{{\pi {x^2}}}{8} = 4x - {x^2} - \frac{{\pi {x^2}}}{8}\).
d) Đúng. \(S\) đạt giá trị lớn nhất khi \(x = \frac{4}{{2 + \frac{\pi }{4}}} = \frac{{16}}{{8 + \pi }}\) nên \(y = 4 - x - \frac{{\pi x}}{4} = \frac{{16}}{{8 + \pi }}\).
Lời giải
a) Đúng. Chi phí để \(A\) sản xuất \(10\) tấn sản phẩm trong một tháng là \(C\left( {10} \right) = 100 + 30.10 = 400\)triệu đồng.
b) Sai. Số tiền \(A\) thu được khi bán \(10\) tấn sản phẩm cho \(B\) là
\(R\left( {10} \right) = 10.P\left( {10} \right) = 10.\left( {45 - 0,{{001.10}^2}} \right) = 449\) triệu đồng.
c) Đúng. Lợi nhuận mà \(A\) thu được là: \(H\left( x \right) = R\left( x \right) - C\left( x \right) = xP\left( x \right) - C\left( x \right)\)
\(P\left( x \right) = 45x - 0,001{x^3} - \left( {100 + 30x} \right) = - 0,001{x^3} + 15x - 100\).
d) Đúng. Xét hàm số \(H\left( x \right) = - 0,001{x^3} + 15x - 100\), \(\left( {0 \le x \le 100} \right)\).
Ta có: \(H'\left( x \right) = - 0,003{x^2} + 15 = 0 \Leftrightarrow - 0,003{x^2} + 15 = 0 \Leftrightarrow x = 50\sqrt 2 \) (chọn).
Khi đó: \(H\left( 0 \right) = - 100\); \[H\left( {50\sqrt 2 } \right) = 500\sqrt 2 - 100\]; \(H\left( {100} \right) = 400\).
Vậy \(A\) bán cho \(B\) khoảng \(50\sqrt 2 \approx 70,7\) tấn sản phẩm mỗi tháng thì thu được lợi nhuận lớn nhất bằng \[H\left( {50\sqrt 2 } \right) = 500\sqrt 2 - 100\].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.