B. Tự luận
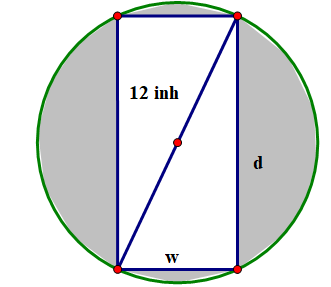
Độ bền \(S\) của dầm gỗ hình chữ nhật tỉ lệ với tích của chiều rộng \(w\) và bình phương chiều sâu \(d\) của nó (xem hinh vẽ). Tìm kích thước của dầm gỗ bền nhất có thể được cắt từ một khúc gỗ hình trụ có đường kính bằng 12 inch.
B. Tự luận
Độ bền \(S\) của dầm gỗ hình chữ nhật tỉ lệ với tích của chiều rộng \(w\) và bình phương chiều sâu \(d\) của nó (xem hinh vẽ). Tìm kích thước của dầm gỗ bền nhất có thể được cắt từ một khúc gỗ hình trụ có đường kính bằng 12 inch.

Quảng cáo
Trả lời:
Từ đề bài suy ra công thức tính độ bền của dầm gỗ có dạng \(S = kw{d^2}\) với hằng số \(k > 0\) cố định nào đó (là hệ số tỉ lệ). Mặt khác, do \({d^2} + {w^2} = 144\) nên ta có \(S = kw\left( {144 - {w^2}} \right) = k\left( {144w - {w^3}} \right)\), \(0 < w < 12\).
Ta có: \(S' = k\left( {144 - 3{w^2}} \right);S' = 0 \Leftrightarrow w = 4\sqrt 3 \) (do \(w > 0\)).
Lập bảng biến thiên của hàm số:
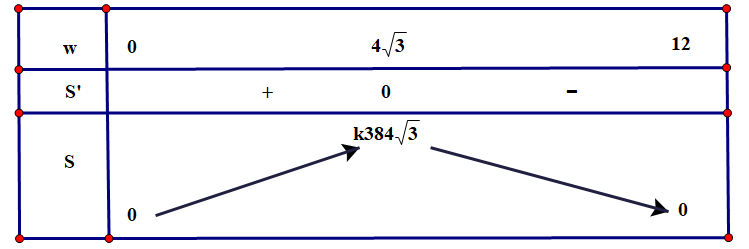
Vậy dầm gỗ có độ bền lớn nhất khi có chiều rộng \(w = 4\sqrt 3 \) inch và chiều sâu \(d = 4\sqrt 6 \) inch.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
a) Đúng. Chi phí mỗi ngày là tổng các chi phí nên \(C\left( x \right) = 0,0005{x^2} + 0,15x + 5\) (triệu đồng).
b) Sai. Khi \(x = 100\), ta có \(C\left( {100} \right) = 0,0005 \times {100^2} + 0,15 \times 100 + 5 = 25\).
c) Sai. Chi phí trung bình trên mỗi khối sản phẩm là:
\(\overline c \left( x \right) = \frac{{0,0005{x^2} + 0,15x + 5}}{x} = 0,0005x + 0,15 + \frac{5}{x}\).
d) Đúng. Xét hàm số \(\overline c \left( x \right) = 0,0005x + 0,15 + \frac{5}{x}\), \(0 < x \le 200\).
Ta có \({\overline c ^{\,\prime }}\left( x \right) = \frac{5}{{{{10}^4}}} - \frac{5}{{{x^2}}}\), \({\overline c ^\prime }\left( x \right) = 0 \Leftrightarrow {x^2} = {10^4} \Rightarrow x = 100\) (do \(x \in \left( {0;200} \right]\).
Bảng biến thiên:
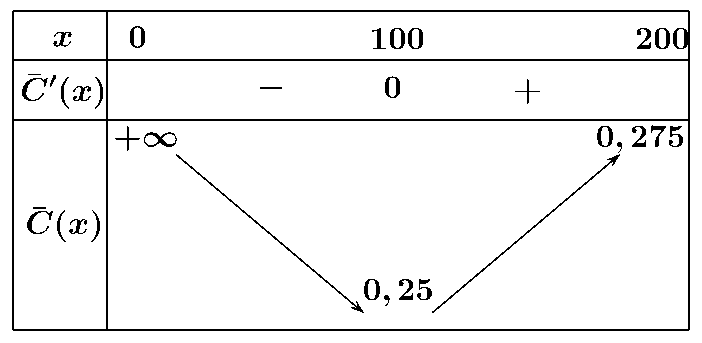
Vậy chi phí trung bình giảm khi hàm số \(\overline c \left( x \right)\)nghịch biến, tức là \(x \in \left( {0;100} \right)\).
Lời giải
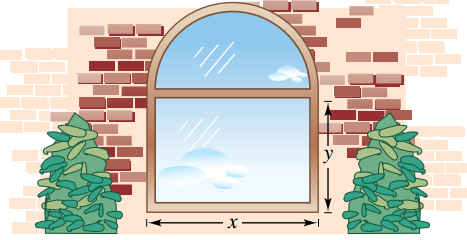
a) Đúng. Bán kính của hình bán nguyệt là \(\frac{x}{2}\) nên nửa chu vi bán nguyệt là \(\frac{{\pi x}}{2}\).
b) Đúng. Ta có \(2\left( {x + y} \right) + \frac{{\pi x}}{2} = 8 \Leftrightarrow y = 4 - \frac{{x\left( {4 + \pi } \right)}}{4}\).
c) Sai. Diện tích của cửa sổ:\(S = xy + \frac{1}{2}\pi {\left( {\frac{x}{2}} \right)^2} = x\left( {4 - x - \frac{{\pi x}}{4}} \right) + \frac{{\pi {x^2}}}{8} = 4x - {x^2} - \frac{{\pi {x^2}}}{8}\).
d) Đúng. \(S\) đạt giá trị lớn nhất khi \(x = \frac{4}{{2 + \frac{\pi }{4}}} = \frac{{16}}{{8 + \pi }}\) nên \(y = 4 - x - \frac{{\pi x}}{4} = \frac{{16}}{{8 + \pi }}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.