Một nhà máy sản xuất \[{\rm{ }}x\] sản phẩm trong mỗi tháng. Chi phí sản xuất \(x\) sản phẩm được cho bởi hàm chi phí \(C\left( x \right) = 16\,000 + 500x - 1,6{x^2} + 0,004{x^3}\) (nghìn đồng). Biết giá bán của của mỗi sản phẩm là một hàm số phụ thuộc vào số lượng sản phẩm \(x\) và được cho bởi công thức \(p\left( x \right) = 1700 - 7x\) (nghìn đồng). Hỏi mỗi tháng nhà máy nên sản xuất bao nhiêu sản phẩm để lợi nhuận thu được là lớn nhất? Biết rằng kết quả khảo sát thị trường cho thấy sản phẩm sản xuất ra sẽ được tiêu thụ hết.
Một nhà máy sản xuất \[{\rm{ }}x\] sản phẩm trong mỗi tháng. Chi phí sản xuất \(x\) sản phẩm được cho bởi hàm chi phí \(C\left( x \right) = 16\,000 + 500x - 1,6{x^2} + 0,004{x^3}\) (nghìn đồng). Biết giá bán của của mỗi sản phẩm là một hàm số phụ thuộc vào số lượng sản phẩm \(x\) và được cho bởi công thức \(p\left( x \right) = 1700 - 7x\) (nghìn đồng). Hỏi mỗi tháng nhà máy nên sản xuất bao nhiêu sản phẩm để lợi nhuận thu được là lớn nhất? Biết rằng kết quả khảo sát thị trường cho thấy sản phẩm sản xuất ra sẽ được tiêu thụ hết.
Câu hỏi trong đề: Đề kiểm tra Toán 12 Chân trời sáng tạo Chương 1 có đáp án !!
Quảng cáo
Trả lời:
Điều kiện \(\left\{ \begin{array}{l}x > 0\\1700 - 7x > 0\end{array} \right. \Leftrightarrow 0 < x < \frac{{1700}}{7}\).
Doanh thu được khi công ty sản xuất và tiêu thụ hết \(x\) sản phẩm là \(R\left( x \right) = xp\left( x \right) = 1700x - 7{x^2}\).
Do đó, lợi nhuận thu được là
\(P\left( x \right) = xp\left( x \right) - C\left( x \right)\)\( = 1700x - 7{x^2} - \left( {16\,000 + 500x - 1,6{x^2} + 0,004{x^3}} \right)\)
\(P\left( x \right) = - 0,004{x^3} - 5,4{x^2} + 1200x - 16\,000\), \(0 < x < \frac{{1700}}{7}\).
\(P'\left( x \right) = - 0,012{x^2} - 10,8x + 1200\); \(P'\left( x \right) = 0 \Leftrightarrow - 0,012{x^2} + 10,8x + 1200 = 0 \Leftrightarrow \left[ \begin{array}{l}x = - 1000\\x = 100\end{array} \right.\).
Đối chiếu điều kiện ta có \(x = 100\).
Lập bảng biến thiên của hàm số, ta thu được kết quả là
\(\mathop {\max }\limits_{\left( {0;\frac{{1700}}{7}} \right)} P\left( x \right) = P\left( {100} \right) = 46\,000\) (nghìn đồng).
Vậy công ty cần sản xuất 100 sản phẩm thì lợi nhuận thu được là cao nhất.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Xét hàm số \(C = \frac{{19200000}}{{{x^2}}} + \frac{{27x}}{{x + 3000}},\,\,\left( {x \ge 1} \right)\) là chi phí đặt hàng và vận chuyển một linh kiện
Ta có \(C' = - \frac{{38400000}}{{{x^3}}} + \frac{{81000}}{{{{\left( {x + 3000} \right)}^2}}}\).
Cho \(C' = 0 \Leftrightarrow 12800{\left( {x + 3000} \right)^2} - 27{x^3} = 0 \Leftrightarrow x = 2400\).
Lập BBT cho hàm số trên nửa khoảng \(\left[ {1; + \infty } \right)\) ta thu được \({C_{\min }}\) khi \(x = 2400\).
Đáp án: 2400.
Câu 2
Lời giải
Chọn D
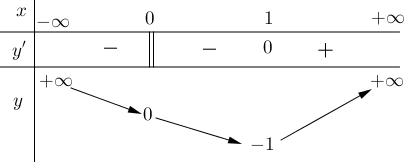
Dựa vào bảng biến thiên, nhận thấy đạo hàm \(y'\) của hàm số chỉ đổi dấu một lần khi \(x\) đi qua \({x_0} = 1\) nên hàm số chỉ có một cực trị duy nhất, do đó phương án D sai.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.