Đề kiểm tra Toán 12 Chân trời sáng tạo Chương 1 có đáp án - Đề 2
26 người thi tuần này 4.6 278 lượt thi 11 câu hỏi 45 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề kiểm tra Công thức xác suất toàn phần – công thức Bayes (có lời giải) - Đề 3
Đề kiểm tra Công thức xác suất toàn phần – công thức Bayes (có lời giải) - Đề 2
Đề kiểm tra Công thức xác suất toàn phần – công thức Bayes (có lời giải) - Đề 1
Đề kiểm tra Xác suất có điều kiện (có lời giải) - Đề 3
Đề kiểm tra Xác suất có điều kiện (có lời giải) - Đề 2
Danh sách câu hỏi:
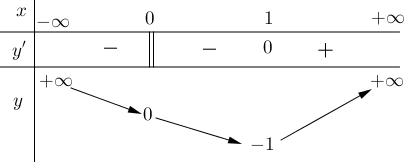
Câu 1
Lời giải
Chọn B
Từ bảng biến thiên, ta thấy hàm số đồng biến trên khoảng \(\left( { - 1;0} \right)\).
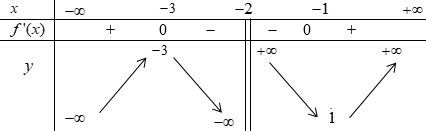
Câu 2
Lời giải
Chọn D
Dựa vào bảng biến thiên, nhận thấy đạo hàm \(y'\) của hàm số chỉ đổi dấu một lần khi \(x\) đi qua \({x_0} = 1\) nên hàm số chỉ có một cực trị duy nhất, do đó phương án D sai.
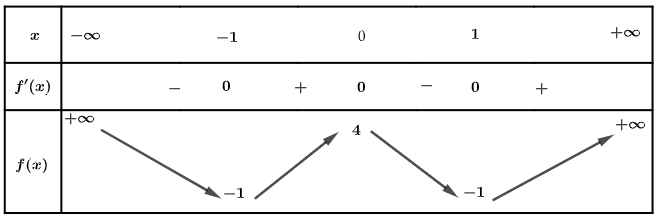
Câu 3
Lời giải
Chọn B
Ta có: \[2f\left( x \right) - 5 = 0 \Leftrightarrow f\left( x \right) = \frac{5}{2}\].
Từ bảng biến thiên của hàm số \(y = f\left( x \right)\) suy ra số nghiệm phương trình \(2f\left( x \right) - 5 = 0\) là \(1\).
Câu 4
Lời giải
Chọn A
Ta có \(\mathop {\lim }\limits_{x \to + \infty } y = 2 \Rightarrow y = 2\) là tiệm cận ngang.
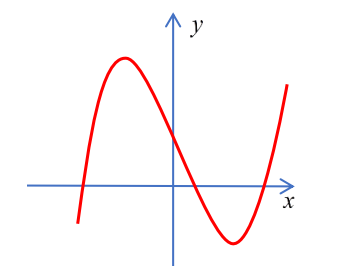
Câu 5
Lời giải
Chọn D
Đồ thị đã cho là đồ thị hàm bậc ba có hệ số \(a > 0\)
(do \(\mathop {\lim }\limits_{x \to + \infty } \left( {a{x^3} + b{x^2} + cx + d} \right) = + \infty \) nếu \(a > 0\) ). Loại A, B.
Đồ thị cắt trục tung tại điểm có tung độ dương nên chọn D.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
![Chọn B Ta có: \[2f\left( x \right) - 5 = 0 \Leftrightarrow f\left( x \right) = \frac{5}{2}\]. Từ bảng biến thiên của hàm số \(y = f\left( x \right)\) suy ra số nghiệm phương trình \(2f\left( x \right) - 5 = 0\) là \(1\). (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/10/15-1759418289.png)
![Chọn C Từ bảng biến thiên suy ra giá trị lớn nhất của \(y = f\left( x \right)\) trên \(\left[ {1;5} \right]\) bằng \(3\). (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/10/17-1759418432.png)