Ta biết rằng Mặt Trăng chuyển động quanh Trái Đất theo quỹ đạo là một elip mà Trái Đất là một tiêu điểm. Elip đó có A1A2 = 768 800 km và B1B2 = 767 619 km (Nguồn: Ron Larson (2014), Precalculus Rea...

Hướng dẫn giải Phương trình chính tắc của elip trên có dạng ( frac{{{x^2}}}{{{a^2}}} + frac{{{y^2}}}{{{b^2}}} = 1 ), trong đó a > b > 0. Ta có Oy là đường trung trực của A1A2 nên O là trung điểm của A1A2 nên OA2 = ( frac{{{A_1}{A_2}}}{2} ) ( = frac{{768 , ,800}}{2} = 384 , ,400 ). Vì điểm A2 nằm trên trục Ox về phía bên phải điểm O và cách O một khoảng bằng 384 400 nên A2(384 800; 0). Elip (E) cắt trục Ox tại A2(384 800; 0), thay vào phương trình elip ta được: ( frac{{384 ,{{800}^2}}}{{{a^2}}} + frac{{{0^2}}}{{{b^2}}} = 1 Leftrightarrow {a^2} = 384 ,{800^2} Rightarrow a = 384 ,800 ) (do a > 0). Lại có Ox là đường trung trực của B1B2 nên O là trung điểm của B1B2 nên OB2 = ( frac{{{B_1}{B_2}}}{2} ) ( = frac{{767 , ,619}}{2} = 338 ,309,5 ). Vì điểm B2 nằm trên trục Oy về phía bên trên điểm O và cách O một khoảng bằng 338309,5 nên B2(0; 338309,5). Elip (E) cắt trục Oy tại B2(0; 338309,5), thay vào phương trình elip ta được: ( frac{{{0^2}}}{{{a^2}}} + frac{{{{338309,5}^2}}}{{{b^2}}} = 1 Leftrightarrow {b^2} = {338309,5^2} Rightarrow b = 338309,5 ) (do b > 0). Vì 384 800 > 338309,5 nên a > b > 0 (thỏa mãn điều kiện). Vậy phương trình chính tắc của elip (E) là ( frac{{{x^2}}}{{{{384800}^2}}} + frac{{{y^2}}}{{{{338309,5}^2}}} = 1 ).

Câu hỏi:

04/07/2022 3,701

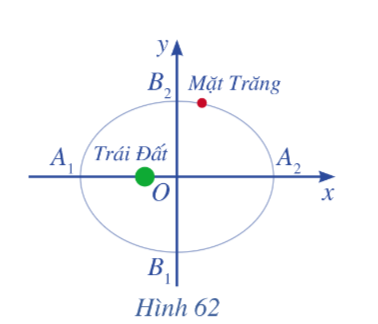
Ta biết rằng Mặt Trăng chuyển động quanh Trái Đất theo quỹ đạo là một elip mà Trái Đất là một tiêu điểm. Elip đó có A₁A₂ = 768 800 km và B₁B₂ = 767 619 km (Nguồn: Ron Larson (2014), Precalculus Real Mathematics, Real People, Cengage) (Hình 62). Viết phương trình chính tắc của elip đó.

Xem lời giải

Câu hỏi trong đề: Bài tập Ba đường conic có đáp án !!

Giao bài

Quảng cáo

Trả lời:

Giải bởi Vietjack

Hướng dẫn giải

Phương trình chính tắc của elip trên có dạng \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\), trong đó a > b > 0.

Ta có Oy là đường trung trực của A₁A₂ nên O là trung điểm của A₁A₂ nên OA₂ = \(\frac{{{A_1}{A_2}}}{2}\)\( = \frac{{768\,\,800}}{2} = 384\,\,400\).

Vì điểm A₂ nằm trên trục Ox về phía bên phải điểm O và cách O một khoảng bằng 384 400 nên A₂(384 800; 0).

Elip (E) cắt trục Ox tại A₂(384 800; 0), thay vào phương trình elip ta được:

\(\frac{{384\,{{800}^2}}}{{{a^2}}} + \frac{{{0^2}}}{{{b^2}}} = 1 \Leftrightarrow {a^2} = 384\,{800^2} \Rightarrow a = 384\,800\) (do a > 0).

Lại có Ox là đường trung trực của B₁B₂ nên O là trung điểm của B₁B₂ nên OB₂ = \(\frac{{{B_1}{B_2}}}{2}\)\( = \frac{{767\,\,619}}{2} = 338\,309,5\).

Vì điểm B₂ nằm trên trục Oy về phía bên trên điểm O và cách O một khoảng bằng 338309,5 nên B₂(0; 338309,5).

Elip (E) cắt trục Oy tại B₂(0; 338309,5), thay vào phương trình elip ta được:

\(\frac{{{0^2}}}{{{a^2}}} + \frac{{{{338309,5}^2}}}{{{b^2}}} = 1 \Leftrightarrow {b^2} = {338309,5^2} \Rightarrow b = 338309,5\) (do b > 0).

Vì 384 800 > 338309,5 nên a > b > 0 (thỏa mãn điều kiện).

Vậy phương trình chính tắc của elip (E) là \(\frac{{{x^2}}}{{{{384800}^2}}} + \frac{{{y^2}}}{{{{338309,5}^2}}} = 1\).

Đang tải chế độ Học...

Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay

ĐẶC QUYỀN VIP

Đăng ký VIP để học và luyện thi không giới hạn

Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.

Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
Đăng ký ngay

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Một chiếc đèn có mặt cắt ngang là hình parabol (Hình 63). Hình parabol có chiều rộng giữa hai mép vành là AB = 40 cm và chiều sâu h = 30 cm (h bằng khoảng cách từ O đến AB). Bóng đèn nằm ở tiêu điểm S. Viết phương trình chính tắc của parabol đó.

Xem đáp án

Lời giải

Hướng dẫn giải

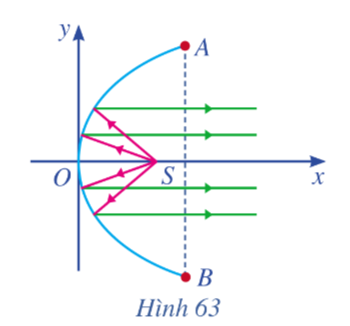
Phương trình chính tắc của parabol có dạng y² = 2px (với p > 0).

Vì AB = 40 và Ox là đường trung trực của đoạn AB nên khoảng cách từ điểm A đến trục Ox là \(\frac{{40}}{2} = 20\).

Chiều sâu h bằng khoảng cách từ O đến AB và cũng chính bằng khoảng cách từ điểm A đến trục Oy và bằng 30.

Do đó, parabol đi qua điểm A có hoành độ là 30 (khoảng cách từ A đến trục Oy) và tung độ là 20 (khoảng cách từ A đến trục Ox) hay A(30; 20).

Thay tọa độ điểm A vào phương trình chính tắc của parabol, ta được:

20² = 2p . 30 ⇔ 60p = 400 ⇔ p = \(\frac{{20}}{3}\) (thỏa mãn p > 0).

Vậy phương trình chính tắc của parabol cần lập là \({y^2} = 2.\frac{{20}}{3}.x\,\,hay\,\,{y^2} = \frac{{40}}{3}x\).

Câu 2

Cho Elip (E) có phương trình chính tắc \(\frac{{{x^2}}}{{49}} + \frac{{{y^2}}}{{25}} = 1.\)Tìm tọa độ các giao điểm của (E) với trục Ox, Oy và tọa độ các tiêu điểm của (E).

Xem đáp án

Lời giải

Hướng dẫn giải

Ta có: \(\frac{{{x^2}}}{{49}} + \frac{{{y^2}}}{{25}} = 1 \Leftrightarrow \frac{{{x^2}}}{{{7^2}}} + \frac{{{y^2}}}{{{5^2}}} = 1.\)

Do a > b > 0 nên elip (E) có a = 7, b = 5.

Ta có: c² = a² – b² = 7² – 5² = 24, suy ra \(c = \sqrt {24} = 2\sqrt 6 \).

Vậy tọa độ các giao điểm của (E) với trục Ox là A₁(– 7; 0), A₂(7; 0), tọa độ các giao điểm của (E) với trục Oy là B₁(0; – 5), B₂(0; 5) và tọa độ các tiêu điểm của E là \({F_1}\left( { - 2\sqrt 6 ;\,\,0} \right),\,\,{F_2}\left( {2\sqrt 6 ;\,\,0} \right)\).

Câu 3