Bài tập Ba đường conic có đáp án
60 người thi tuần này 5.0 14.6 K lượt thi 29 câu hỏi
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề kiểm tra Ôn tập chương 9 (có lời giải) - Đề 3
Đề kiểm tra Ôn tập chương 9 (có lời giải) - Đề 2
Đề kiểm tra Ôn tập chương 9 (có lời giải) -Đề 1
Đề kiểm tra Thực hành tính xác suất theo định nghĩa cổ điển (có lời giải) - Đề 3
Đề kiểm tra Thực hành tính xác suất theo định nghĩa cổ điển (có lời giải) - Đề 2
Đề kiểm tra Thực hành tính xác suất theo định nghĩa cổ điển (có lời giải) - Đề 1
Đề kiểm tra Biến cố và định nghĩa cổ điển của xác suất (có lời giải) -Đề 2
Đề kiểm tra Biến cố và định nghĩa cổ điển của xác suất (có lời giải) -Đề 2
Danh sách câu hỏi:
Lời giải
Hướng dẫn giải
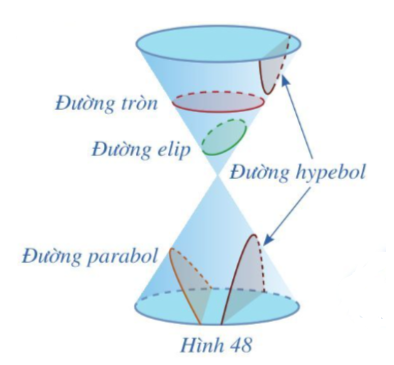
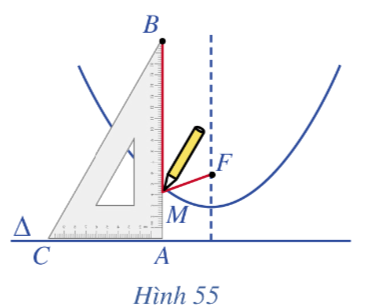
Sau bài học này ta sẽ biết đường conic gồm đường parabol, đường elip, đường hypebol và cách xác định phương trình chính tắc của mỗi loại đường conic trên.
Lời giải
Hướng dẫn giải
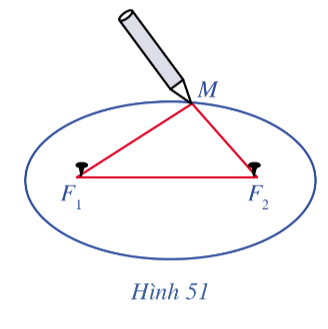
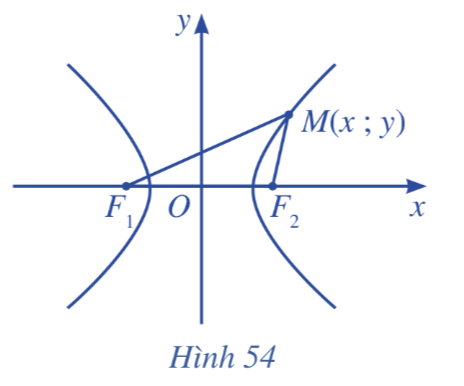
Theo bài ra ta thấy tổng MF1 + MF2 luôn bằng độ dài vòng dây kín, do đó khi M thay đổi, tổng MF1 + MF2 là một độ dài không đổi.
Lời giải
Hướng dẫn giải
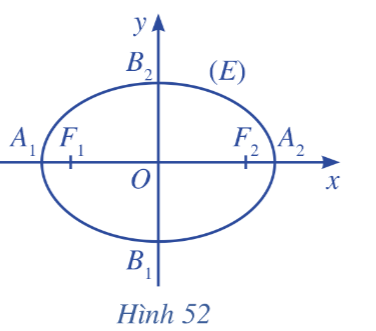
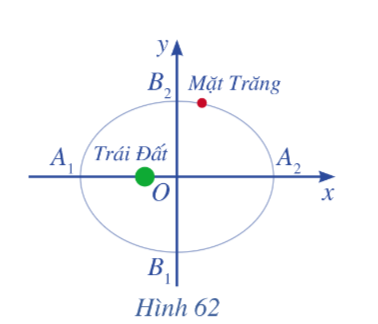
Ta có: \({A_1}{F_1} = \sqrt {{{\left( {\left( { - c} \right) - \left( { - a} \right)} \right)}^2} + {{\left( {0 - 0} \right)}^2}} = \left| { - c + a} \right|\) = a – c (do a > c > 0).
\({A_1}F{ & _2} = \sqrt {{{\left( {c - \left( { - a} \right)} \right)}^2} + {{\left( {0 - 0} \right)}^2}} = \left| {a + c} \right|\) = a + c
Do đó: A1F1 + A2F2 = a – c + a + c = 2a.
Vậy điểm A1(– a; 0) thuộc elip (E).
Mà A1(– a; 0) thuộc trục Ox nên A1(– a; 0) là giao điểm của elip (E) với trục Ox.
Tương tự, ta chứng minh được A2(a; 0) là giao điểm của elip (E) với trục Ox.
Lời giải
Hướng dẫn giải:
Vì \(b = \sqrt {{a^2} - {c^2}} \) nên \({b^2} = {a^2} - {c^2} \Leftrightarrow {a^2} = {b^2} + {c^2}\).
Ta có: \({B_2}{F_1} = \sqrt {{{\left( { - c - 0} \right)}^2} + {{\left( {0 - b} \right)}^2}} = \sqrt {{c^2} + {b^2}} = \sqrt {{a^2}} = a\) (do a > 0).
\({B_2}{F_2} = \sqrt {{{\left( {c - 0} \right)}^2} + {{\left( {0 - b} \right)}^2}} = \sqrt {{c^2} + {b^2}} = \sqrt {{a^2}} = a\) (do a > 0).
Do đó B2F1 = B2F2 = a nên B2F1 + B2F2 = a + a = 2a. Do đó, B2(0; b) thuộc elip (E).
Mà B2(0; b) thuộc trung Oy nên B2(0; b) là giao điểm của elip (E) với trục Oy.
Tương tự, ta chứng minh được B1(0; – b) là giao điểm của elip (E) với trục Oy.
Lời giải
Hướng dẫn giải
Elip (E) có phương trình chính tắc là: \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\,\,\left( {a > b > 0} \right)\).
Do elip (E) đi qua điểm M(0; 3) nên tọa độ điểm M thỏa mãn phương trình elip, do đó ta có \(\frac{{{0^2}}}{{{a^2}}} + \frac{{{3^2}}}{{{b^2}}} = 1 \Leftrightarrow {b^2} = {3^2} \Rightarrow b = 3\) (do b > 0).
Do elip (E) đi qua điểm \(N\left( {3; - \frac{{12}}{5}} \right)\) nên tọa độ điểm N thỏa mãn phương trình elip, do đó ta có \(\frac{{{3^2}}}{{{a^2}}} + \frac{{{{\left( { - \frac{{12}}{5}} \right)}^2}}}{{{3^2}}} = 1 \Leftrightarrow {a^2} = 25 \Rightarrow a = 5\) (do a > 0).
Vậy elip (E) có phương trình chính tắc là: \(\frac{{{x^2}}}{{25}} + \frac{{{y^2}}}{9} = 1\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.