Câu hỏi:
12/07/2024 2,125
Cho đường thẳng xx’, điểm A thuộc xx’. Trên tia Ax’ lấy điểm B (điểm B khác điểm A). Vẽ tia By, trên tia By lấy điểm M. Hai điểm N và P thảo mãn: \(\widehat {NMA} = \widehat {MAB};\widehat {PMy} = \widehat {MBx'}\) (H.3.21) Giải thích tại sao ba điểm N; M; P thẳng hàng.
Quảng cáo
Trả lời:
Giải bởi Vietjack
Lời giải:
Theo đề bài ra ta có:
\(\widehat {NMA} = \widehat {MAB}\), mà hai góc này ở vị trí so le trong, suy ra MN // xx;
\(\widehat {PMy} = \widehat {MBx'}\), mà hai góc này ở vị trí đồng vị, suy ra MP // xx’
Theo tiên đề Euclid, qu điểm M chỉ có một đường thẳng song song với xx’. Mà MN và NP cùng song song với xx’ nên MN vag MP trùng nhau.
Do đó, ba điểm M, N, P thẳng hàng.
Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Lời giải:
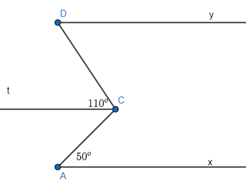
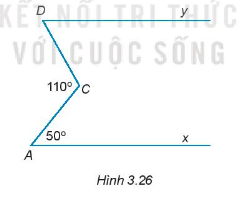
Kẻ tia Ct song song với Ax nên Ct song song với Dy (do Ax // Dy)
Vì Ax // Ct và \(\widehat {CAx}\) và \(\widehat {ACt}\) là hai góc so le trong nên \(\widehat {CAx}\) = \(\widehat {ACt}\) = 50o.
Ta lại có:
\(\widehat {ACt}\) + \(\widehat {tCD}\) = 110o
50o + \(\widehat {tCD}\) = 110o
\(\widehat {tCD}\) =110o – 50o
\(\widehat {tCD}\) = 60o
Vì Ct // By và \(\widehat {tCD}\) và \(\widehat {CDy}\) là hai góc so le trong nên \(\widehat {tCD}\) = \(\widehat {CDy}\) = 60o.
Vậy \(\widehat {CDy}\) = 60o.
Lời giải
Lời giải:
Phát biểu diễn đạt đúng nội dung tiên đề Euclid là phát biểu b và phát biểu d.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
Đề kiểm tra cuối học kỳ 2 Toán 7 Kết nối tri thức có đáp án - Đề 1
-
Bộ 7 đề thi học kì 2 Toán lớp 7 Chân trời sáng tạo có đáp án - Đề 04
-
Đề kiểm tra cuối học kỳ 2 Toán 7 Kết nối tri thức có đáp án - Đề 2
-
15 câu Trắc nghiệm Toán 7 Kết nối tri thức Bài 1: Tập hợp các số hữu tỉ có đáp án
-
Bộ 7 đề thi học kì 2 Toán lớp 7 Chân trời sáng tạo có đáp án - Đề 01
-
Bộ 7 đề thi học kì 2 Toán 7 Cánh Diều có đáp án - Đề 01
-
Bộ 7 đề thi học kì 2 Toán lớp 7 Chân trời sáng tạo có đáp án - Đề 02
-
Đề thi giữa học kì 2 Toán 7 KNTT - Đề 01 có đáp án