Câu hỏi:
13/07/2024 991
Gọi Bx, Cy lần lượt là tia phân giác của các góc BE và ACF. Chứng minh rằng Bxx // Cy.
Gọi Bx, Cy lần lượt là tia phân giác của các góc BE và ACF. Chứng minh rằng Bxx // Cy.
Câu hỏi trong đề: Giải SBT Toán 7 Ôn tập chương 3 có đáp án !!
Bắt đầu thiQuảng cáo
Trả lời:
Giải bởi Vietjack
Hướng dẫn giải:
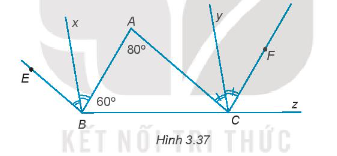
Vì Bx là tia phân giác của góc \(\widehat {ABE}\) nên \(\widehat {EBx} = \widehat {xBA} = \frac{{\widehat {EBA}}}{2} = \frac{{80^\circ }}{2} = 40^\circ \)
Vì Cy là tia phân giác của góc \(\widehat {ACF}\) nên \(\widehat {ACy} = \widehat {yCF} = \frac{{\widehat {ACF}}}{2} = \frac{{80^\circ }}{2} = 40^\circ \)
Ta có BC cắt Bx và cắt Cy tạo ra cặp góc đồng vị là \[\widehat {zCy}\] và \(\widehat {zBx}\).
Ta có:
\[\widehat {zCy}\] = \(\widehat {yCF}\)+ \(\widehat {FCz}\) = 40o + 60o = 100o.
\(\widehat {zBx}\)= \(\widehat {xBA}\)+ \(\widehat {ABC}\) = 40o + 60o = 100o.
Suy ra, \[\widehat {zCy}\] = \(\widehat {zBx}\)= 100o
Vì \[\widehat {zCy}\] và \(\widehat {zBx}\) là hai góc đồng vị và \[\widehat {zCy}\] = \(\widehat {zBx}\) nên Bx // Cy.
Nhà sách vietjack
Hot: Đề thi cuối kì 2 Toán, Văn, Anh.... file word có đáp án chi tiết lớp 1-12 form 2025 (chỉ từ 100k). Tải ngay
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Cho Hình 3.36. Bên trong góc BOD vẽ tia Ox song song với AB. Biết \(\widehat B = 40^\circ ;\widehat D = 70^\circ ;\widehat {BOD} = 110^\circ \).
Tính số đo của góc BOx.
Cho Hình 3.36. Bên trong góc BOD vẽ tia Ox song song với AB. Biết \(\widehat B = 40^\circ ;\widehat D = 70^\circ ;\widehat {BOD} = 110^\circ \).
Tính số đo của góc BOx.
Xem đáp án »
13/07/2024
1,810
Câu 2:
A. Câu hỏi (trắc nghiệm)
Cho hai góc kề bù AOB và BOC. Tia OM nằm giữa hai tia OB và OC. Tia ON là tia đối của tia OM. Khi đó cặp góc đối đỉnh là cặp góc nào trong các cặp góc sau đây?
Xem đáp án »
05/07/2022
1,728
Câu 3:
Cho Hình 3.35. Biết CN là tia phân giác của góc ACM.
Chứng minh rằng CN // AB.
Xem đáp án »
13/07/2024
1,655
Câu 4:
Hai đường thẳng AB và CD cắt nhau tại O. Cho OM là tia phân giác của góc BOD và \(\widehat {BOM} = 30^\circ \). Số đo của góc AOC bằng:
Xem đáp án »
05/07/2022
1,653
Câu 6:
Hai đường thẳng cắt nhau tạo thành bốn góc khác góc bẹt. Số đo của bốn góc đó có thể là trường hợp nào trong các trường hợp sau đây?
Xem đáp án »
05/07/2022
1,146
🔥 Đề thi HOT:
-
15 câu Trắc nghiệm Toán 7 Kết nối tri thức Bài 1: Tập hợp các số hữu tỉ có đáp án
-
Đề kiểm tra cuối học kỳ 2 Toán 7 Kết nối tri thức có đáp án - Đề 1
-
Bộ 7 đề thi học kì 2 Toán lớp 7 Chân trời sáng tạo có đáp án - Đề 04
-
Bộ 5 đề thi Giữa kì 2 Toán 7 Cánh diều cấu trúc mới có đáp án - Đề 01
-
Bộ 5 đề thi Giữa kì 2 Toán 7 Chân trời sáng tạo cấu trúc mới có đáp án - Đề 01
-
12 Bài tập Một số bài toán thực tế liên quan đại lượng tỉ lệ thuận (có lời giải)
-
12 Bài tập Một số bài toán thực tế liên quan đại lượng tỉ lệ nghịch (có lời giải)
-
15 câu Trắc nghiệm Toán 7 Chân trời sáng tạo Bài 1: Tập hợp các số hữu tỉ có đáp án
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận