Giải SBT Toán 7 Ôn tập chương 3 có đáp án
26 người thi tuần này 4.6 1.5 K lượt thi 19 câu hỏi
🔥 Đề thi HOT:
15 câu Trắc nghiệm Toán 7 Kết nối tri thức Bài 1: Tập hợp các số hữu tỉ có đáp án
16.3 K lượt thi
15 câu hỏi
5 câu Trắc nghiệm Tập hợp các số hữu tỉ có đáp án (Nhận biết)
4.1 K lượt thi
5 câu hỏi
Bộ 12 Đề thi học kì 2 Toán 7 Kết nối tri thức cấu trúc mới có đáp án - Đề 1
18.3 K lượt thi
17 câu hỏi
15 câu Trắc nghiệm Toán 7 Cánh diều Bài 1: Tập hợp Q các số hữu tỉ có đáp án
4.3 K lượt thi
15 câu hỏi
17 Bài tập Tập hợp các số hữu tỉ (có lời giải)
1.1 K lượt thi
17 câu hỏi
15 câu Trắc nghiệm Toán 7 Chân trời sáng tạo Bài 1: Tập hợp các số hữu tỉ có đáp án
4 K lượt thi
15 câu hỏi
Đề thi giữa học kì 2 Toán 7 KNTT - Đề 01 có đáp án
3 K lượt thi
39 câu hỏi
10 Bài tập Các bài toán thực tế giải bằng cách lập đa thức (có lời giải)
693 lượt thi
10 câu hỏi
Nội dung liên quan:
Danh sách câu hỏi:
Lời giải
Lời giải:
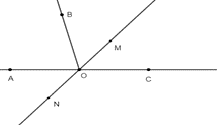
Từ hình vẽ ta thấy cặp góc đối đỉnh là \(\widehat {AOM}\) và \(\widehat {CON}\) vì OA là tia đối của tia OC và OM là tia đối của tia ON.
Đáp án đúng là C.
Lời giải
Lời giải:
Khẳng định đúng là: Hai góc đối đỉnh thì bằng nhau.
Đáp án đúng là C.
Lời giải
Lời giải:
Giả sử: đừng thẳng a cắt đường thẳng b tại O, tạo thành 4 góc \(\widehat {{O_1}};\widehat {{O_2}};\widehat {{O_3}};\widehat {{O_4}}\) và \(\widehat {{O_1}}\) = 65o.
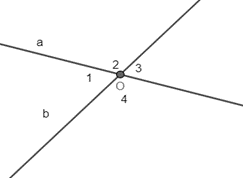
Vì \(\widehat {{O_1}}\) và \(\widehat {{O_3}}\) đối đỉnh nên \(\widehat {{O_1}}\) = \(\widehat {{O_3}}\) = 65o.
Vì \(\widehat {{O_3}}\) và \(\widehat {{O_4}}\) kề bù nên \(\widehat {{O_3}}\) + \(\widehat {{O_4}}\) = 180o.
Thay số: 65o + \(\widehat {{O_4}}\) = 180o
\(\widehat {{O_4}}\) = 180o – 65o = 115o.
Mà \(\widehat {{O_4}}\) và \(\widehat {{O_2}}\) đối đỉnh nên \(\widehat {{O_4}}\) = \(\widehat {{O_2}}\) = 115o.
Vậy \(\widehat {{O_4}}\) = \(\widehat {{O_2}}\) = 115o; \(\widehat {{O_1}}\) = \(\widehat {{O_3}}\) = 65o.
Đáp án đúng là D.
Lời giải
Lời giải:
Vì hai đường thẳng cắt nhau tạo thành bốn góc khác góc bẹt nên sẽ có hai cặp góc đối đỉnh.
Mà các góc đối đỉnh thì bằng nhau. Do đó, trong bốn giá trị sẽ lần lượt có hai cặp giá trị góc bằng nhau.
Nhận thấy chỉ có đáp án D thỏa mãn.
Vậy đáp án đúng là D.
Lời giải
Lời giải:
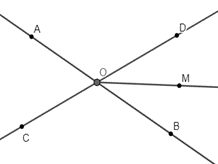
Vì OM là tia phân giác của góc BOD nên \(\widehat {BOM} = \widehat {MOD} = \frac{{\widehat {BOD}}}{2} = 30^\circ \)
Suy ra \(\widehat {BOD}\) = 2.30o = 60o.
Lại có, \(\widehat {BOD}\) và \(\widehat {AOC}\) là hai góc đối đỉnh nên \(\widehat {BOD}\) = \(\widehat {AOC}\) = 60o.
Đáp án đúng là B.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo