15 câu Trắc nghiệm Bài ôn tập cuối chương 4 có đáp án (Thông hiểu)
17 người thi tuần này 4.6 1.6 K lượt thi 15 câu hỏi 30 phút
🔥 Đề thi HOT:
Bộ 12 Đề thi học kì 2 Toán 7 Kết nối tri thức cấu trúc mới có đáp án - Đề 1
15 câu Trắc nghiệm Toán 7 Kết nối tri thức Bài 1: Tập hợp các số hữu tỉ có đáp án
15 câu Trắc nghiệm Toán 7 Cánh diều Bài 1: Tập hợp Q các số hữu tỉ có đáp án
15 câu Trắc nghiệm Toán 7 Chân trời sáng tạo Bài 1: Tập hợp các số hữu tỉ có đáp án
Đề kiểm tra cuối học kỳ 2 Toán 7 Kết nối tri thức có đáp án - Đề 2
Bộ 10 đề thi giữa kì 1 Toán 7 Kết nối tri thức cấu trúc mới có đáp án - Đề 1
Bộ 12 đề thi học kì 2 Toán lớp 7 Chân trời sáng tạo cấu trúc mới có đáp án - Đề 04
5 câu Trắc nghiệm Tập hợp các số hữu tỉ có đáp án (Nhận biết)
Nội dung liên quan:
Danh sách câu hỏi:
Lời giải
Hướng dẫn giải
Đáp án đúng là: D
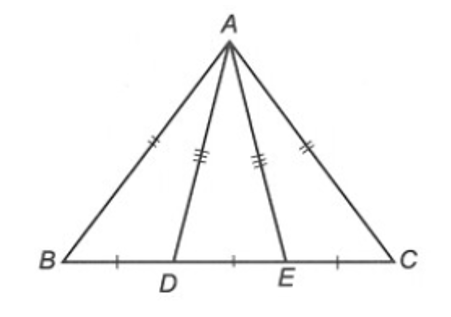
⦁ Ta có BD = EC (giả thiết)
Suy ra BD + DE = DE + EC.
Khi đó BE = CD.
Vì vậy phương án A đúng.
⦁ Xét ∆ABE và ∆ACD, có:
AB = AC (giả thiết)
AD = AE (giả thiết)
BE = CD (chứng minh trên)
Do đó ∆ABE = ∆ACD (c.c.c)
Vì vậy phương án B đúng.
⦁ Ta có ∆ABE = ∆ACD (chứng minh trên)
Suy ra (cặp góc tương ứng)
Do đó phương án C đúng.
Vậy ta chọn phương án D.
Lời giải
Hướng dẫn giải
Đáp án đúng là: B
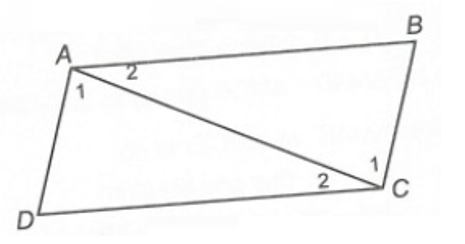
Xét ∆ABC và ∆CDA, có:
AC là cạnh chung.
(do AD // BC và hai góc này ở vị trí so le trong)
(do AB // DC và hai góc này ở vị trí so le trong)
Do đó ∆ABC = ∆CDA (g.c.g)
Vậy có 1 cặp tam giác bằng nhau.
Do đó ta chọn phương án B.
Lời giải
Hướng dẫn giải
Đáp án đúng là: C
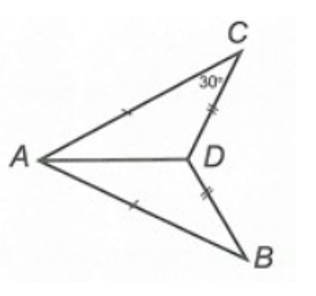
Ta có . Suy ra .
∆MNP có (định lí tổng ba góc trong một tam giác)
Suy ra .
Do đó .
Vì vậy .
Vậy ta chọn phương án C.
Lời giải
Hướng dẫn giải
Đáp án đúng là: B
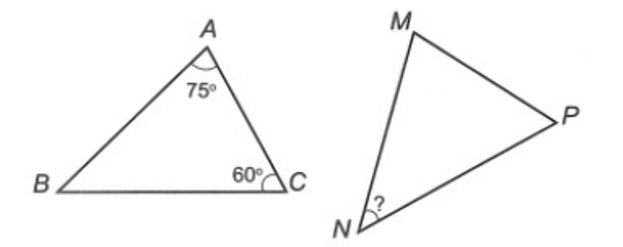
∆ABC có: (định lí tổng ba góc trong một tam giác)
Suy ra .
Ta có ∆ABC = ∆MNP (giả thiết)
Suy ra (cặp góc tương ứng)
Vậy ta chọn phương án B.
Lời giải
Hướng dẫn giải
Đáp án đúng là: D
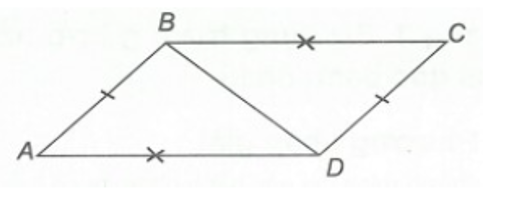
Xét ∆ABD và ∆CDB, có:
BD là cạnh chung.
AB = CD (giả thiết)
AD = CB (giả thiết)
Do đó ∆ABD = ∆CDB (c.c.c)
Vậy ta chọn phương án D.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.