Đề ôn thi ĐGNL ĐHSP Hà Nội môn Toán có đáp án - Đề số 5
47 người thi tuần này 4.6 292 lượt thi 25 câu hỏi 45 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề ôn thi Hóa học ĐGNL ĐHSP Hà Nội có đáp án - Đề số 5
Đề ôn thi Hóa học ĐGNL ĐHSP Hà Nội có đáp án - Đề số 4
Đề ôn thi Hóa học ĐGNL ĐHSP Hà Nội có đáp án - Đề số 3
Đề ôn thi Hóa học ĐGNL ĐHSP Hà Nội có đáp án - Đề số 2
Đề ôn thi Hóa học ĐGNL ĐHSP Hà Nội có đáp án - Đề số 1
Đề ôn thi ĐGNL ĐHSP Hà Nội môn Toán có đáp án - Đề số 5
Đề ôn thi ĐGNL ĐHSP Hà Nội môn Toán có đáp án - Đề số 4
Đề ôn thi ĐGNL ĐHSP Hà Nội môn Toán có đáp án - Đề số 3
Danh sách câu hỏi:
Lời giải
Điều kiện: \(x > 3\).
Ta có \({\log _2}\left( {x - 1} \right) + {\log _2}\left( {x - 3} \right) = 3\)\( \Leftrightarrow {\log _2}\left( {x - 1} \right)\left( {x - 3} \right) = 3\)\( \Leftrightarrow {x^2} - 4x - 5 = 0\)\( \Leftrightarrow \left[ \begin{array}{l}x = - 1{\rm{ }}(l)\\x = 5{\rm{ (n)}}\end{array} \right.\).
Vậy \(x = 5\). Chọn A.
Câu 2
Lời giải
Ta có diện tích hình phẳng giới hạn bởi đồ thị hàm số \[y = {x^2} - 2x,\,y = - 2{x^2} + 2x\] và hai đường thẳng \[x = 0,\,x = 1\] là \[\int\limits_0^1 {\left| {\left( {{x^2} - 2x} \right) - \left( { - 2{x^2} + 2x} \right)} \right|} \,{\rm{d}}x = 1\]. Chọn A.
Câu 3
Lời giải
Ta có \({\rm{sin}}3x = \frac{1}{2} \Leftrightarrow {\rm{sin}}3x = \sin \frac{\pi }{6} \Leftrightarrow \left[ \begin{array}{l}3x = \frac{\pi }{6} + k2\pi \\3x = \pi - \frac{\pi }{6} + k2\pi \end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = \frac{\pi }{{18}} + \frac{{k2\pi }}{3}\\x = \frac{{5\pi }}{{18}} + \frac{{k2\pi }}{3}\end{array} \right.\) \(\left( {k \in \mathbb{Z}} \right)\). Chọn A.
Câu 4
Lời giải
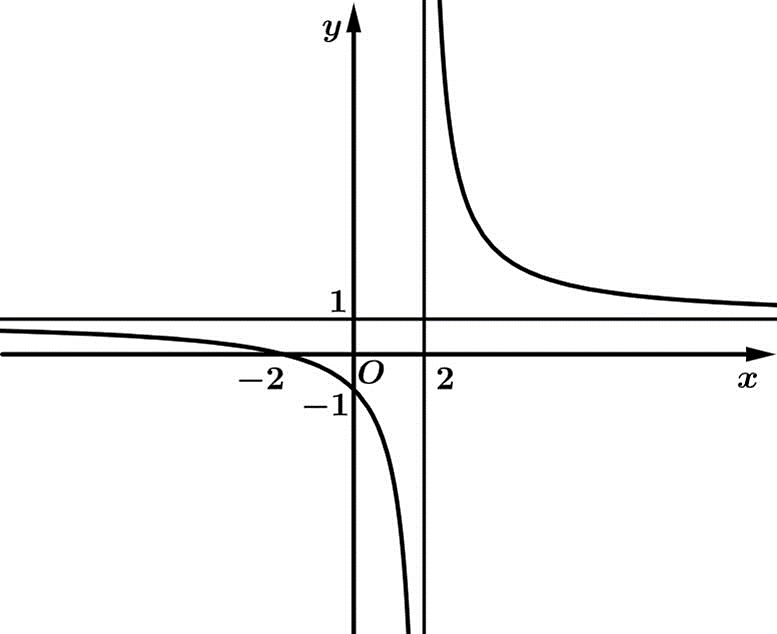
Tiệm cận ngang \(y = a \Rightarrow a = 1\).
Tiệm cận đứng \(x = - c \Rightarrow c = - 2\).
Giao điểm với trục tung \(y = \frac{b}{c} = \frac{b}{{ - 2}} = - 1 \Rightarrow b = 2\).
Vậy \(P = 2{\rm{a}} - b + 3c = 2 - 2 - 6 = - 6\). Chọn B.
Câu 5
Lời giải
Phương trình tham số của đường phân giác trong góc \[A\]: \[\left\{ \begin{array}{l}x = t\\y = 6 - 4t\\z = 6 - 3t\end{array} \right.\] \[\left( d \right)\].
Gọi \[D\] là điểm đối xứng với \[M\] qua \[\left( d \right)\]. Khi đó \[D \in AC\]\[ \Rightarrow \] đường thẳng \[AC\]có một vectơ chỉ phương là \[\overrightarrow {ND} \].
Ta xác định điểm \[D\].
Gọi \[K\] là giao điểm \[MD\] với \[\left( d \right)\]. Ta có \[K\left( {t;\,6 - 4t;\,6 - 3t} \right)\]; \[\overrightarrow {MK} = \left( {t;\,1 - 4t;\,3 - 3t} \right)\].
Ta có \[\overrightarrow {MK} \bot {\vec u_d}\] với \[{\vec u_d} = \left( {1;\, - 4;\, - 3} \right)\] nên \[t - 4\left( {1 - 4t} \right) - 3\left( {3 - 3t} \right) = 0\]\[ \Leftrightarrow t = \frac{1}{2}\].
Suy ra \[K\left( {\frac{1}{2};\,4;\frac{9}{2}} \right)\], mà \[K\] là trung điểm \[MD\] nên \[\left\{ \begin{array}{l}{x_D} = 2{x_K} - {x_M}\\{y_D} = 2{y_K} - {y_M}\\{z_D} = 2{z_K} - {z_M}\end{array} \right.\]\[ \Leftrightarrow \left\{ \begin{array}{l}{x_D} = 1\\{y_D} = 3\\{z_D} = 6\end{array} \right.\] hay \[D\left( {1;\,3;\,6} \right)\].
Một vectơ chỉ phương của \[AC\]là \[\overrightarrow {DN} = \left( {0;\, - 2;\, - 6} \right)\]. Hay \[\vec u = \left( {0;\,1;\,3} \right)\] là vectơ chỉ phương. Chọn B.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 8
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 9
A. \(12,67\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 10
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 11
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 13
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 14
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 15
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 16
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 17
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 18
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.