30 câu Trắc nghiệm Toán 7 Kết nối tri thức Bài tập cuối chương 3 có đáp án
68 người thi tuần này 4.6 2 K lượt thi 30 câu hỏi 30 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
15 câu Trắc nghiệm Toán 7 Kết nối tri thức Bài 1: Tập hợp các số hữu tỉ có đáp án
Bộ 5 đề thi Cuối kì 1 Toán 7 Kết nối tri thức cấu trúc mới có đáp án - Đề 1
15 câu Trắc nghiệm Toán 7 Chân trời sáng tạo Bài 1: Tập hợp các số hữu tỉ có đáp án
Bộ 5 đề thi Cuối kì 1 Toán 7 Kết nối tri thức cấu trúc mới có đáp án - Đề 2
Bộ 5 đề thi Cuối kì 1 Toán 7 Kết nối tri thức cấu trúc mới có đáp án - Đề 3
Bộ 5 đề thi học kì 1 Toán 7 Cánh diều cấu trúc mới có đáp án - Đề 1
Bộ 5 đề thi giữa kì 1 Toán 7 Kết nối tri thức cấu trúc mới có đáp án - Đề 1
Bộ 5 đề thi Cuối kì 1 Toán 7 Kết nối tri thức cấu trúc mới có đáp án - Đề 4
Nội dung liên quan:
Danh sách câu hỏi:
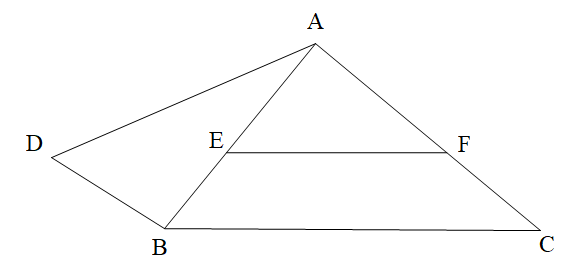
Câu 1
A. 50°;
B. 40°;
C. 60°;
D. 30°.
Lời giải
Đáp án đúng là: D
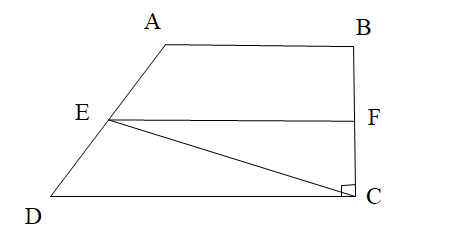
Vì EF // DC nên ta có: \[\widehat {ECD} = \widehat {F{\rm{E}}C}\] (hai góc so le trong)
Ta có \[\widehat {BCD} = 90^\circ \] hay \[\widehat {FCE} + \widehat {ECD} = 90^\circ \] suy ra \[\widehat {ECD} = 90^\circ - 60^\circ = 30^\circ \].
Do đó \[\widehat {FEC} = \widehat {ECD} = 30^\circ \].
Vậy chọn đáp án D.
Câu 2
A. \[\widehat {ABC}\] và \[\widehat {ADC}\] là hai góc kề bù;
B. \[\widehat {AOB}\] và \[\widehat {BOC}\] là hai góc so le trong;
C. \[\widehat {BAD}\] và \[\widehat {ADC}\] là hai góc đồng vị;
D. \[\widehat {AOB}\] và \[\widehat {DOC}\] là hai góc đối đỉnh.
Lời giải
Đáp án đúng là: D
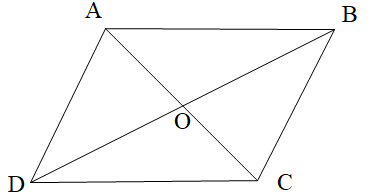
\[\widehat {ABC}\] và \[\widehat {ADC}\] là hai góc kề bù là phát biểu sai vì hai góc này không chung đỉnh.
\[\widehat {AOB}\] và \[\widehat {BOC}\] là hai góc so le trong là phát biểu sai, vì \[\widehat {AOB}\] và \[\widehat {BOC}\] là hai góc kề bù;
\[\widehat {BAD}\] và \[\widehat {ADC}\] là hai góc đồng vị là phát biểu sai, vì \[\widehat {BAD}\] và \[\widehat {ADC}\] là hai góc trong cùng phía.
\[\widehat {AOB}\] và \[\widehat {DOC}\] là hai góc đối đỉnh là phát biểu đúng, chọn phương án D.
Câu 3
A. 60°;
B. 34°;
C. 40°;
D. 84°.
Lời giải
Đáp án đúng là: B.
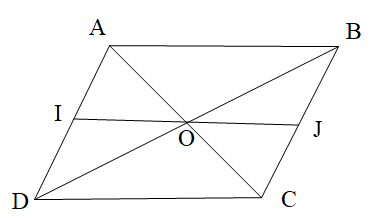
Vì DC // IJ nên ta có: \[\widehat {JOC} = \widehat {OCD}\] (hai góc so le trong).
Do đó \[\widehat {OCD} = \widehat {JOC} = 34^\circ \].
Vậy chọn đáp án B.
Câu 4
A. 60°;
B. 40°;
C. 30°;
D. 125°.
Lời giải
Đáp án đúng là: B
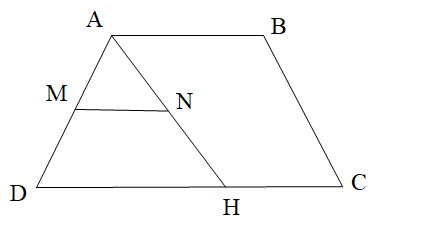
Vì MN // DC do đó \(\widehat {ANM} = \widehat {AHD}\) (hai góc đồng vị).
Mà \[\widehat {ANM} = 40^\circ \] nên \[\widehat {AHD} = 40^\circ \].
Vậy chọn đáp án B.
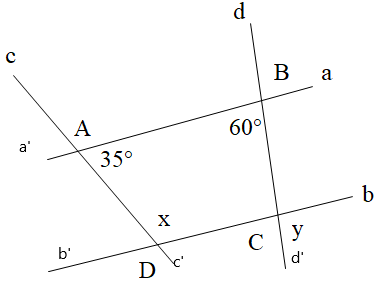
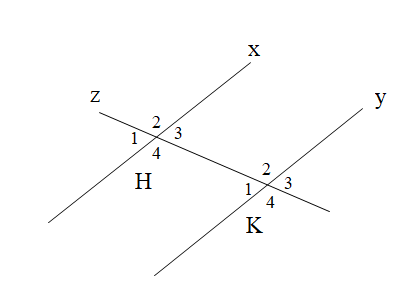
Câu 5
A. x = 60° và y = 35°;
B. x = 120° và y = 145°;
C. x = 35° và y = 60°;
D. x = 145° và y = 120°.
Lời giải
Đáp án đúng là: D
Vì a // b nên \[\widehat {BAD} = \widehat {ADb'} = 35^\circ \] (hai góc so le trong)
Mà \[\widehat {ADb'}\] và \[\widehat {ADC}\] là hai góc kề bù nên suy ra \[\widehat {ADC} + \widehat {ADb'} = 180^\circ \Rightarrow x + 35^\circ = 180^\circ \]
Suy ra, x = 180o ‒ 35° = 145°
Vì a // b nên \[\widehat {ABC} = \widehat {BCb} = 60^\circ \] (hai góc trong so le trong)
Mà \[\widehat {BCb}\] và \[\widehat {bCd'}\] là hai góc kề bù nên suy ra \[\widehat {BCb} + \widehat {bCd'} = 180^\circ \Rightarrow 60^\circ + y = 180^\circ \]
Suy ra \[y = 180^\circ - 60^\circ = 120^\circ \]
Vậy x = 145° và y = 120°.
Câu 6
A. 152°;
B. 143°;
C. 45°;
D. 35°.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A. 145°;
B. 80°;
C. 156°;
D. 134°.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
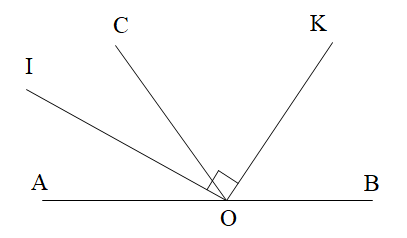
Câu 8
A. Kết luận: \[OI \bot OK\].
B. Kết luận: Cho góc bẹt AOB và tia OI; tia OJ là tia phân giác góc BOK, OK là tia phân giác AOI.
C. Kết luận: Cho góc bẹt AOB và tia OI; tia OJ là tia phân giác góc BOI, OK là tia phân giác AOK.
D. Kết luận: \[OB \bot OK\].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 9
A. Chứng minh định lí đó đúng;
B. Chứng minh định lí đó đúng trong trường hợp cụ thể của giả thiết;
C. Chứng minh định lí đó đúng trong mọi trường hợp có thể xảy ra của giả thiết;
D. Chứng minh định lí đó đúng trong một vài trường hợp cụ thể của giả thiết.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
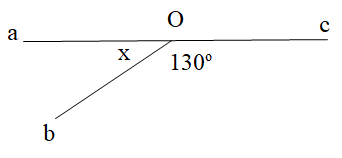
Câu 11
A. hai góc đối đỉnh;
B. hai góc đồng vị;
C. hai góc kề bù;
D. hai góc so le trong.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
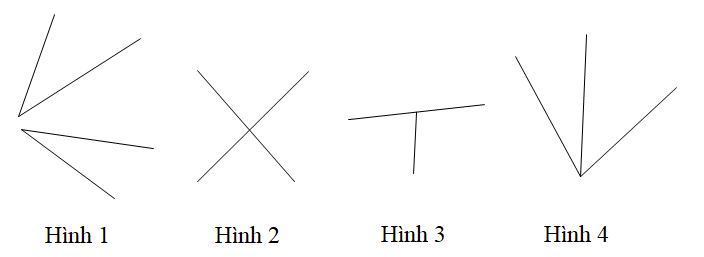
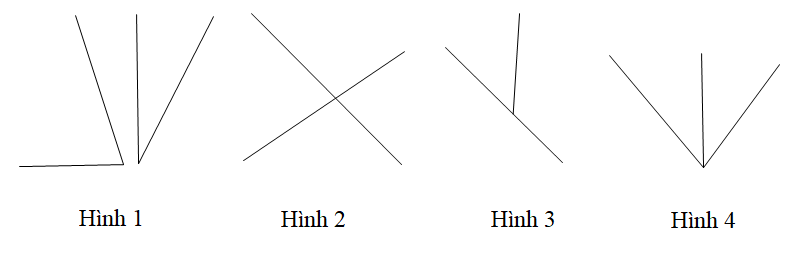
Câu 12
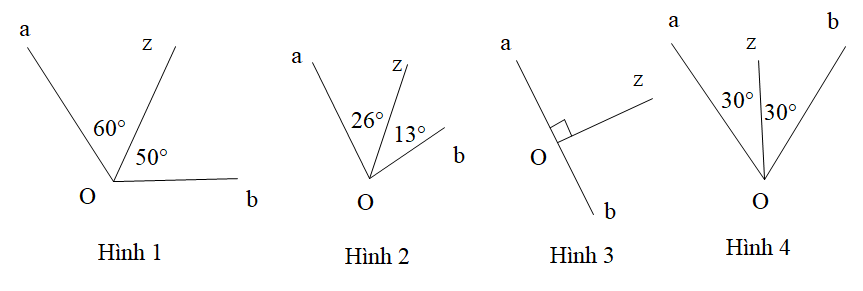
A. Hình 1;
B. Hình 2;
C. Hình 3;
D. Hình 4.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 13
A. Hình 1, Hình 3;
B. Hình 2, Hình 4;
C. Hình 3, Hình 4;
D. Hình 4, Hình 1.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 14
A. \[\widehat {m'On'}\]
B. \[\widehat {m'On}\]
C. \[\widehat {mOn'}\]
D. \[\widehat {mOn}\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 15
A. a // b;
B. \[b \bot c\];
C. \[a \bot b\];
D. Cả 3 đáp án đều sai.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 17
A. 50o;
B. 60o;
C. 65o;
D. 85o.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 18
A. Ba cặp;
B. Bốn cặp;
C. Một cặp;
D. Vô số cặp.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 19
A. 149°;
B. 136°;
C. 70°;
D. 64°.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 20
A. 180°;
B. 141°;
C. 120°;
D. 138°.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
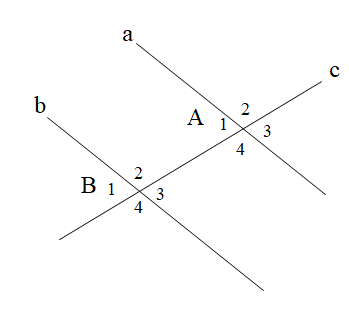
Câu 21
A. \[\widehat {DAB}\] và \[\widehat {EAD}\] là hai góc so le trong;
B. \[\widehat {AFE}\] và \[\widehat {BAC}\] là hai góc so le trong;
C. \[\widehat {AFE}\] và \[\widehat {ACB}\] là hai góc đồng vị;
D. \[\widehat {BAC}\] và \[\widehat {DAB}\] là hai góc đồng vị.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 22
A. 51°;
B. 129°;
C. 138°;
D. 48°.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 23
A. x = 60° và y = 35°;
B. x = 120° và y = 145°;
C. x = 35° và y = 60°;
D. x = 145° và y = 120°.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 24
A. 152°;
B. 143°;
C. 45°;
D. 35°.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 25
Phát biểu định lí sau bằng lời.
|
Giả thiết |
t cắt m tại A, t cắt n tại B \[\widehat {{A_1}}\] và \[\widehat {{B_1}}\]là hai góc đồng vị \[\widehat {{A_1}} = \widehat {{B_1}}\] |
|
Kết luận |
m // n |
A. Nếu đường thẳng t cắt hai đường thẳng m, n và trong số các góc tạo thành có một cặp góc đồng vị bằng nhau thì hai đường thẳng m, n vuông góc với nhau;
B. Nếu đường thẳng t cắt hai đường thẳng m, n và trong số các góc tạo thành có một cặp góc đồng vị bằng nhau thì hai đường thẳng m, n song song với nhau;
C. Nếu đường thẳng t cắt hai đường thẳng m, n và trong số các góc tạo thành có một cặp góc so le trong bằng nhau thì hai đường thẳng m, n song song với nhau;
D. Nếu đường thẳng t cắt hai đường thẳng m, n và trong số các góc tạo thành có một cặp góc so le trong bằng nhau thì hai đường thẳng m, n vuông góc với nhau.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 26
A. Hình 1;
B. Hình 2;
C. Hình 3;
D. Hình 4.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 27
A. \[x = y = 35^\circ \];
B. \[x = 35^\circ ;y = 45^\circ \];
C. \[x = 45^\circ ;y = 35^\circ \];
D. \[x = y = 70^\circ \].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
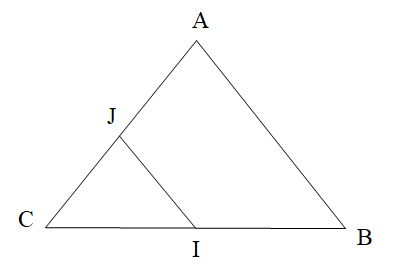
Câu 28
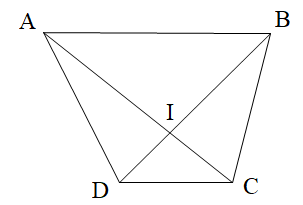
A. \[\widehat {AID}\]và \[\widehat {CIB}\] là hai góc kề bù;
B. \[\widehat {ABC}\] và \[\widehat {ADC}\] là hai góc kề bù;
C. \[\widehat {AIB}\] và \[\widehat {BIC}\] là hai góc kề bù;
D. \[\widehat {AIB}\] và \[\widehat {DIC}\] là hai góc kề bù.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
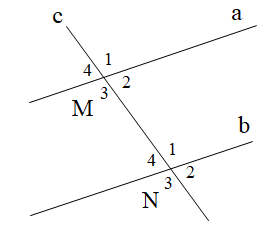
Câu 29
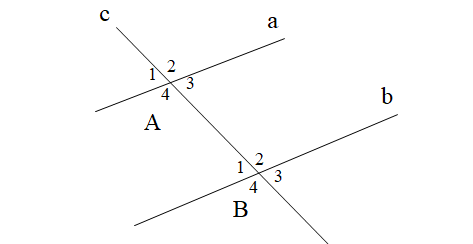
A.
|
Giả thiết |
c cắt a tại A, c cắt b tại B \[\widehat {{A_4}}\] và \[\widehat {{B_2}}\] là hai góc so le trong \[\widehat {{A_4}} = \widehat {{B_2}}\] |
|
Kết luận |
a // b |
B.
|
Giả thiết |
c cắt a tại A, c cắt b tại B \[\widehat {{A_3}}\] và \[\widehat {{B_1}}\] là hai góc đối đỉnh \[\widehat {{A_3}} = \widehat {{B_1}}\] |
|
Kết luận |
a // b |
C.
|
Giả thiết |
c cắt a tại A, c cắt b tại B \[\widehat {{A_3}}\] và \[\widehat {{B_1}}\] là hai góc so le trong \[\widehat {{A_3}} \ne \widehat {{B_1}}\] |
|
Kết luận |
a // b |
D.
|
Giả thiết |
c cắt a tại A, c cắt b tại B \[\widehat {{A_3}}\] và \[\widehat {{B_1}}\] là hai góc đồng vị \[\widehat {{A_3}} \ne \widehat {{B_1}}\] |
|
Kết luận |
a // b |
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 30
A. kết luận;
B. khẳng định;
C. chứng minh;
D. Cả 3 đáp án đều đúng.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.