Câu hỏi trong đề: Giải SBT Toán 7 Bài tập cuối chương 7 có đáp án !!
Quảng cáo
Trả lời:
Cách 1: Xét đa thức P(x) = x3 + 64.
• Với x = 0 thay vào P(x) ta có:
P(0) = 03 + 64 = 64.
Do đó x = 0 không là nghiệm của P(x).
• Với x = 4 thay vào P(x) ta có:
P(4) = 43 + 64 = 64 + 64 = 128.
Do đó x = 4 không là nghiệm của P(x).
• Với x = –4 thay vào P(x) ta có:
P(–4) = (–4)3 + 64 = –64 + 64 = 0.
Do đó x = –4 là nghiệm của P(x).
Vậy trong các số thuộc tập hợp {0; 4; –4} thì có –4 là nghiệm của P(x).
Cách 2: Xét đa thức P(x) = x3 + 64.
Ta có P(x) = 0
Hay x3 + 64 = 0
Suy ra x3 = –64 = (–4)3
Do đó x = –4.
Vậy trong các số thuộc tập hợp {0; 4; –4} thì số –4 là nghiệm của P(x).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
(3x3 – 2x2 + 3x – 2) : (x2 + 1)
Thực hiện đặt tính phép chia đa thức như sau:
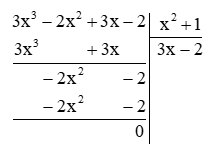
Vậy (3x3 – 2x2 + 3x – 2) : (x2 + 1) = 3x – 2.
Lời giải
(2x3 + 3x2 + 3x + 4) : (x2 + 2).
Thực hiện đặt tính phép chia đa thức như sau:
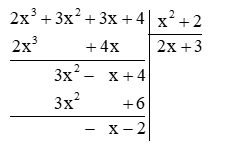
Vậy \(\frac{{2{x^3} + 3{x^2} + 3x + 4}}{{{x^2} + 2}} = 2x + 3 - \frac{{x + 2}}{{{x^2} + 2}}.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.