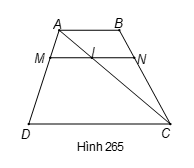
Cho hình thang . Một đường thẳng song song với hai đáy, cắt các cạnh bên AD và BC theo thứ tự ở M và N. Chứng minh rằng:
Cho hình thang . Một đường thẳng song song với hai đáy, cắt các cạnh bên AD và BC theo thứ tự ở M và N. Chứng minh rằng:
Quảng cáo
Trả lời:
Giải bởi Vietjack
Áp dụng định lí Ta-lét vào hai tam giác ACD và ACB ta có ta được
(3); (4).
Cộng theo vế các đẳng thức (3) và (4), thu được:
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
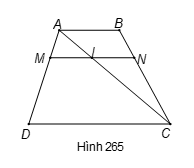
Gọi I là giao điểm của đường chéo AC với MN.
Áp dụng định lí Ta-lét vào hai tam giác ACD và ACB
có , ta được:
(1); (2).
Từ (1) và (2) suy ra: .
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
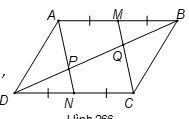
Áp dụng định nghĩa và giả thiết vào hình bình hành ,
ta được:
.
Tứ giác có hai cạnh đối song song và bằng nhau nên
nó là hình bình hành, do đó , suy ra
.
Áp dụng định lí Ta-lét vào hai tam giác và có , ta được:
(1).
(2)
Từ (1) và (2) ta có: .
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập