Dạng 3. Chứng minh các hệ thức hình học có đáp án
28 người thi tuần này 4.6 3.5 K lượt thi 3 câu hỏi 45 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Bộ 10 đề thi giữa kì 2 Toán 8 Chân trời sáng tạo có đáp án - Đề 10
365 lượt thi
9 câu hỏi
Bộ 10 đề thi giữa kì 2 Toán 8 Chân trời sáng tạo có đáp án - Đề 09
319 lượt thi
9 câu hỏi
Bộ 10 đề thi giữa kì 2 Toán 8 Chân trời sáng tạo có đáp án - Đề 08
318 lượt thi
9 câu hỏi
Bộ 10 đề thi giữa kì 2 Toán 8 Chân trời sáng tạo có đáp án - Đề 07
312 lượt thi
9 câu hỏi
Bộ 10 đề thi giữa kì 2 Toán 8 Chân trời sáng tạo có đáp án - Đề 06
311 lượt thi
9 câu hỏi
Bộ 10 đề thi giữa kì 2 Toán 8 Chân trời sáng tạo có đáp án - Đề 05
317 lượt thi
11 câu hỏi
Bộ 10 đề thi giữa kì 2 Toán 8 Chân trời sáng tạo có đáp án - Đề 04
317 lượt thi
11 câu hỏi
Bộ 10 đề thi giữa kì 2 Toán 8 Chân trời sáng tạo có đáp án - Đề 03
318 lượt thi
11 câu hỏi
Danh sách câu hỏi:
Lời giải
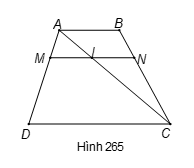
Gọi I là giao điểm của đường chéo AC với MN.
Áp dụng định lí Ta-lét vào hai tam giác ACD và ACB
có , ta được:
(1); (2).
Từ (1) và (2) suy ra: .
Lời giải
Áp dụng định lí Ta-lét vào hai tam giác ACD và ACB ta có ta được
(3); (4).
Cộng theo vế các đẳng thức (3) và (4), thu được:
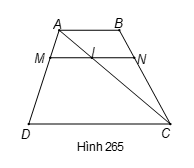
Lời giải
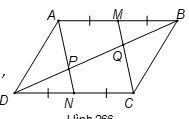
Áp dụng định nghĩa và giả thiết vào hình bình hành ,
ta được:
.
Tứ giác có hai cạnh đối song song và bằng nhau nên
nó là hình bình hành, do đó , suy ra
.
Áp dụng định lí Ta-lét vào hai tam giác và có , ta được:
(1).
(2)
Từ (1) và (2) ta có: .
Nhắn tin Zalo
Hỏi bài tập