Cho hình thang ABCD (AB//CD). Một đường thẳng qua giao điểm O của hai đường chéo và song song với hai đáy, cắt BC ở I. Chứng minh rằng .
Cho hình thang ABCD (AB//CD). Một đường thẳng qua giao điểm O của hai đường chéo và song song với hai đáy, cắt BC ở I. Chứng minh rằng .
Quảng cáo
Trả lời:
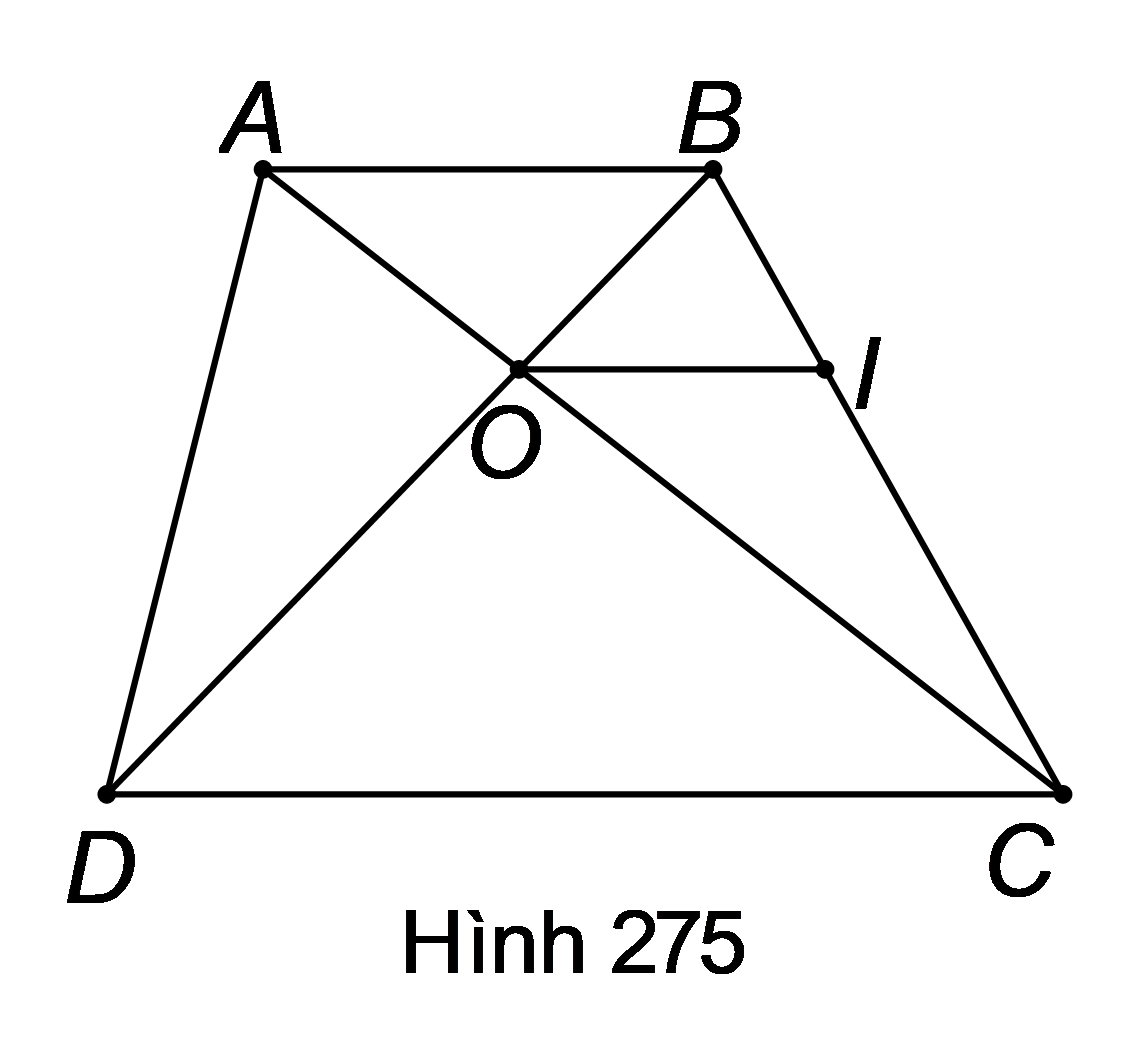
Áp dụng hệ quả của định lí Ta-lét cho , ta được:
(1); (2).
Cộng theo vế các đẳng thức (1) và (2), ta được:
.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
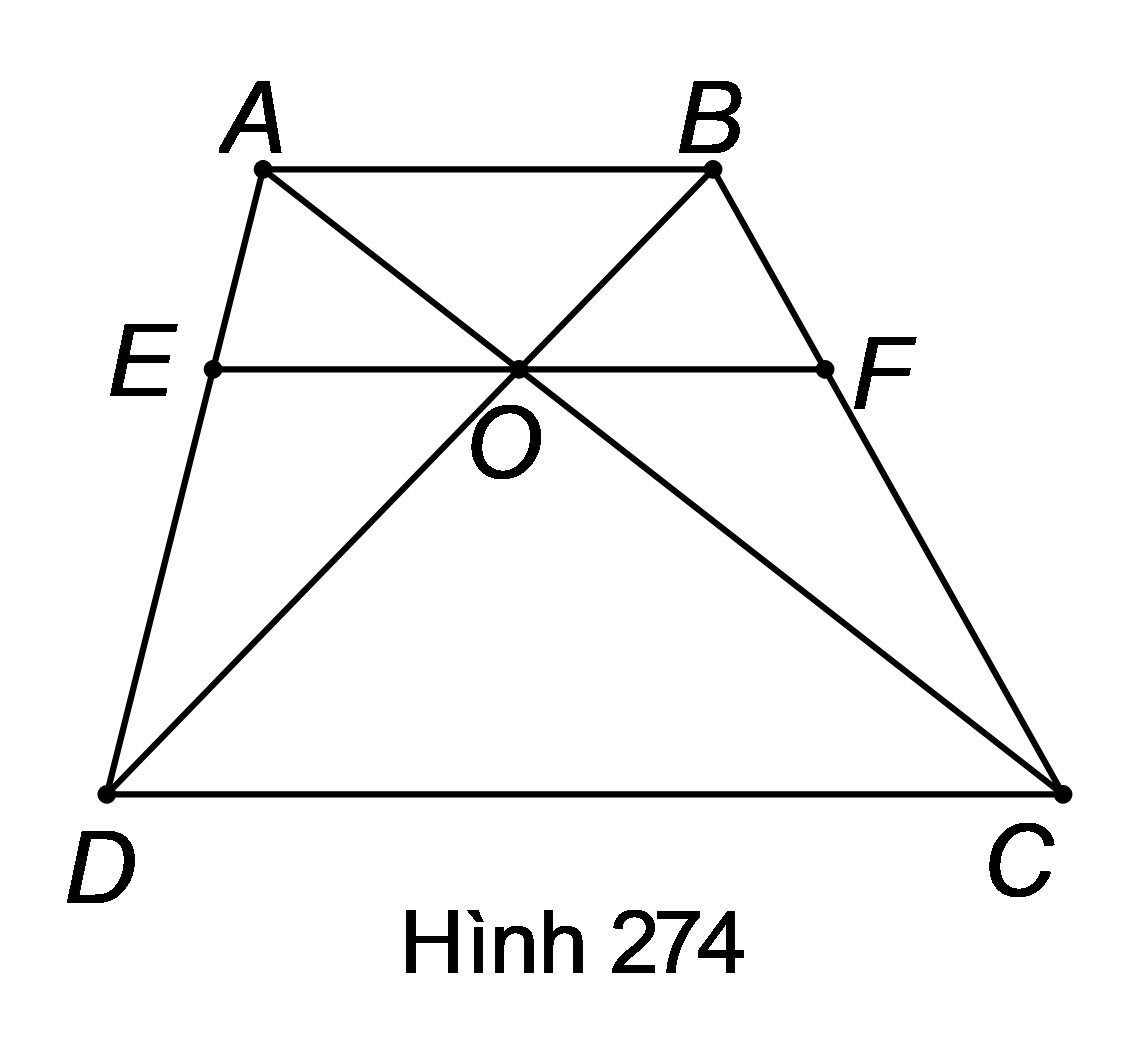
Áp dụng hệ quả của định lí Ta-lét cho và , ta được:
Lời giải
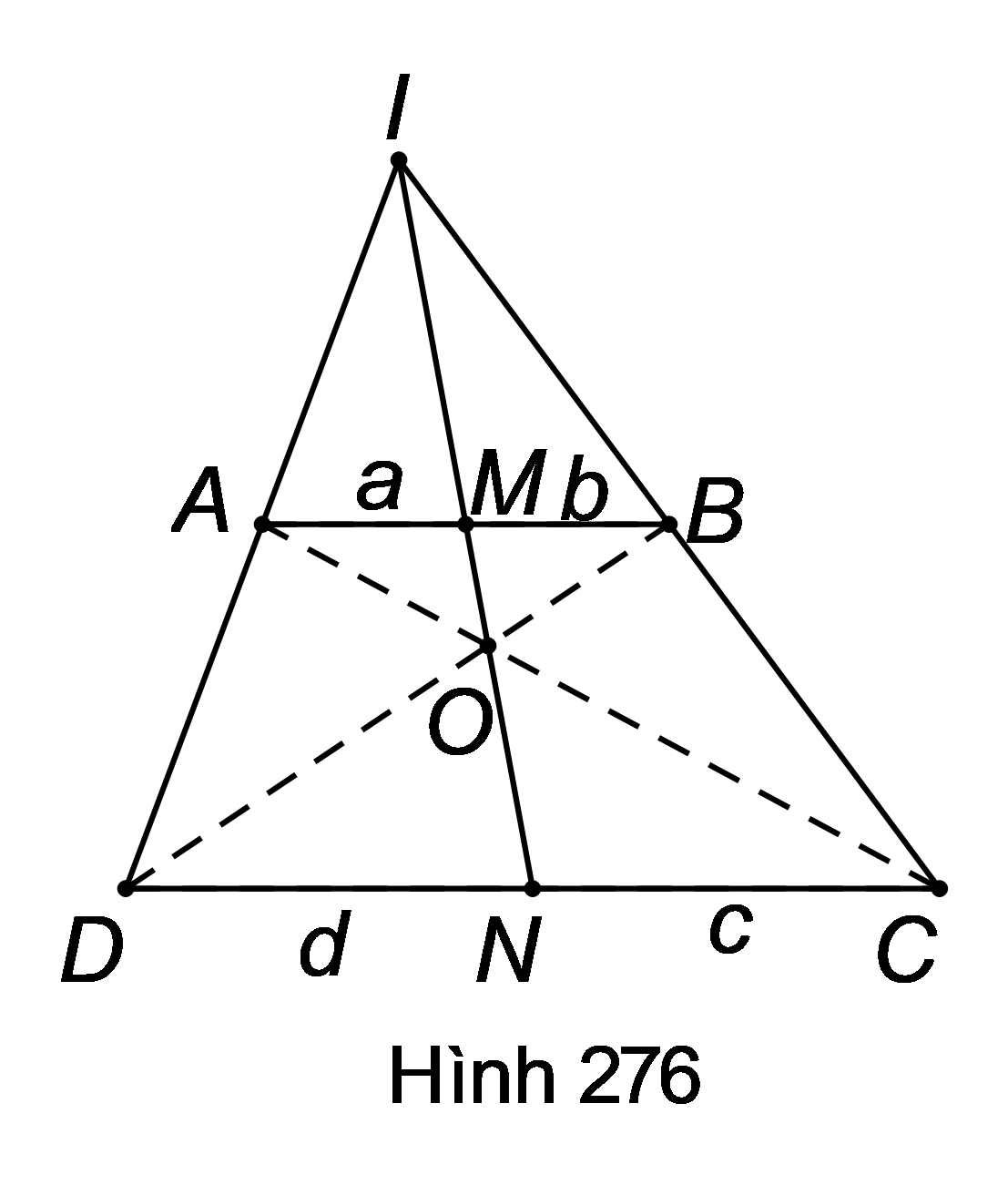
Đặt .
Ta phải chứng minh .
Áp dụng hệ quả của định lí Ta-lét cho và , ta được:
, hay (1);
, hay (2).
Nhân theo vế các đẳng thức (1) và (2) ta được .
Thay vào (1) ta được .
Nhận xét: Trong một hình thang có hai đáy không bằng nhau thì giao điểm của hai cạnh bên, giao điểm của hai đường chéo và trung điểm của hai đáy là bốn điểm thẳng hàng.
Đây chính là nội dung của: Bổ đề về hình thang.