Cho hình thang ABCD và điểm E trên cạnh bên BC. Qua C vẽ đường thẳng song song với AE cắt AD ở K. Chứng minh rằng BK//DE.
Cho hình thang ABCD và điểm E trên cạnh bên BC. Qua C vẽ đường thẳng song song với AE cắt AD ở K. Chứng minh rằng BK//DE.
Quảng cáo
Trả lời:
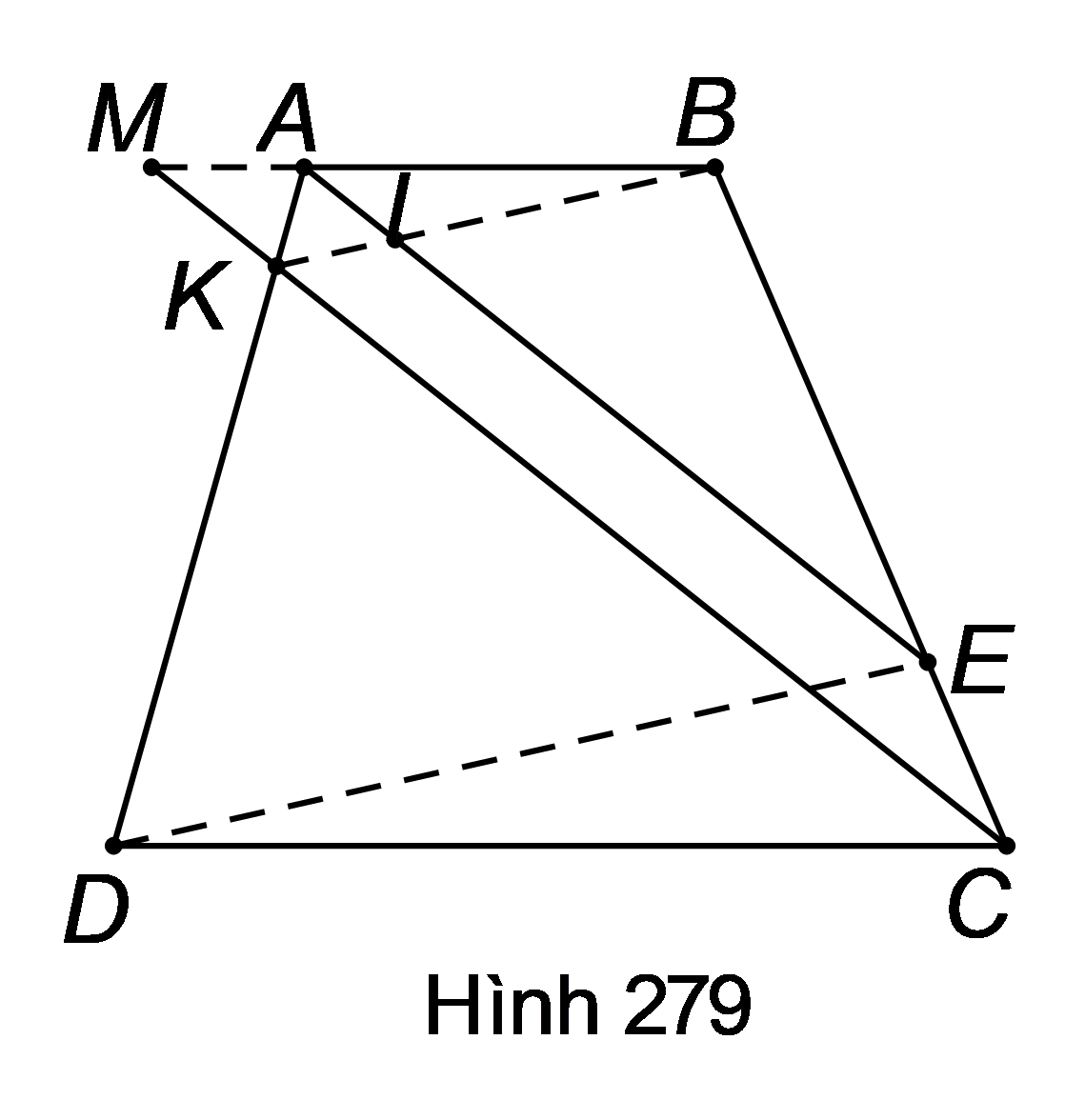
Gọi I,M lần lượt là giao điểm của AE với BK và CK với AB.
Áp dụng hệ quả của định lí Ta-lét cho và , thu được:
(1).
Áp dụng hệ quả của định lí Ta-lét cho , ta được:
(2).
Từ (1) và (2) suy ra . Điều này chứng tỏ đường thẳng KI cắt hai cạnh của tam giác ADE và định ra trên hai cạnh này những đoạn thẳng tương ứng tỉ lệ nên , hay (theo định lí Ta-lét đảo).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
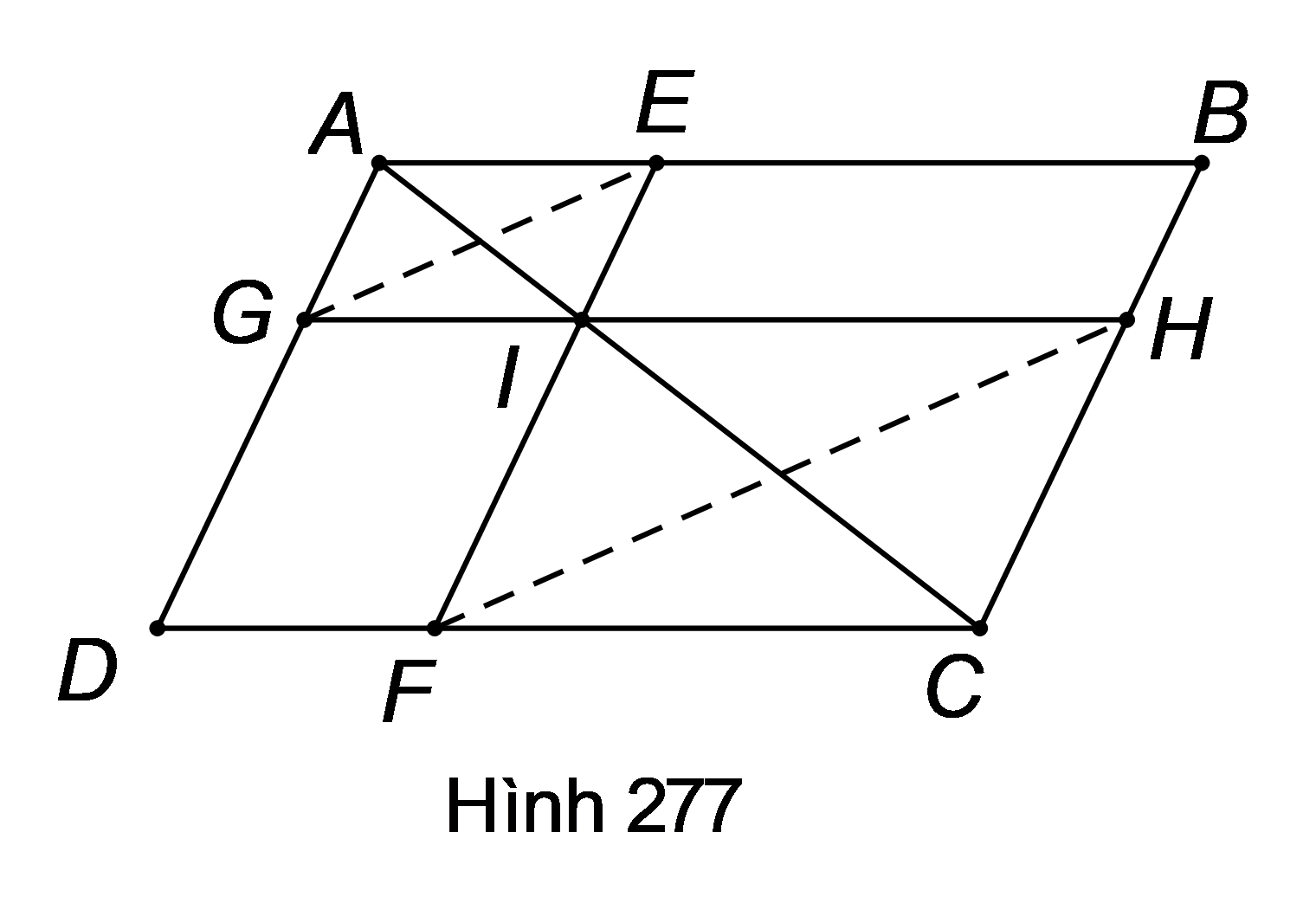
ABCD là hình bình hành nên và , suy ra .
Áp dụng hệ quả của định lí Ta-lét cho và , ta được:
.
Điều này chứng tỏ đường thẳng EG cắt hai cạnh của tam giác IHF và định ra trên hai cạnh này những đoạn thẳng tương ứng tỉ lệ, nên (theo định lí Ta-lét đảo).
Lời giải
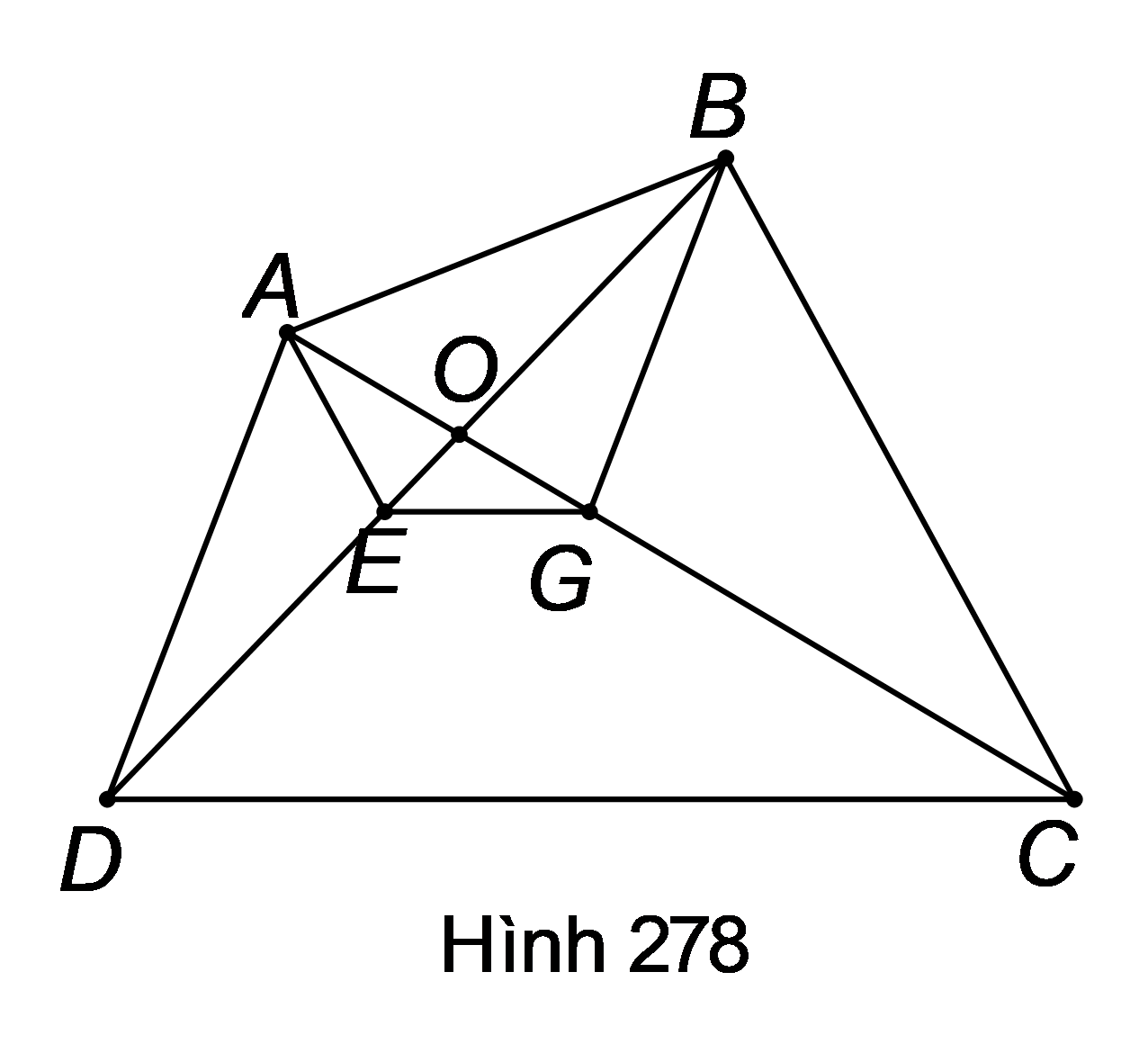
Áp dụng hệ quả của định lí Ta-lét cho và , ta được:
(1); (2).
Nhân theo vế các đẳng thức (1) và (2), ta được:
.
Điều này chứng tỏ đường thẳng EG cắt hai cạnh của tam giác OCD và định ra trên hai cạnh này những đoạn thẳng tương ứng tỉ lệ nên (theo định lí Ta-lét đảo).