Cho tam giác vuông ABC ( = 90°). Lấy M bất kì trên cạnh Gọi E, F lần lượt là các điếm đối xứng với M qua AB và AC. Chứng minh: A là trung điểm của EF.
Câu hỏi trong đề: Bài tập Toán 8 Chủ đề 7: Đối xứng trục có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
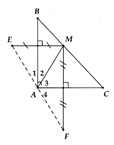
Sử dụng tính chất đối xứng trục Þ AE = AF (=AM) (1).
Sử dụng tính chất của tam giác cân . Từ đó chỉ ra được thằng hàng (2).
Từ (1) và (2) ta có điều phải chứng minh.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
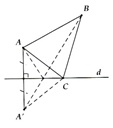
Gọi A' là điểm đối xứng của A qua d => A' cố định.
Vì C Î d => CA = CA' (tính chất đối xứng trục). Ta có:
PABC = AB + AC + BC
= AB + (CA' + CB) AB + BA' (không đổi. Dấu "=" xảy ra tức là chu vi tam giác nhỏ nhất khi C là giao điểm của d và BA'.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập