b) Gọi G là giao điểm của BM và EK. Chứng minh rằng G là trọng tâm của hai tam giác ABC và tam giác DEF.
b) Gọi G là giao điểm của BM và EK. Chứng minh rằng G là trọng tâm của hai tam giác ABC và tam giác DEF.
Câu hỏi trong đề: Bài tập Toán 8 Chủ đề 9: Đối xứng tâm có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
b) Gọi G là giao điểm của EK, BM. I, H là trung điểm của BG, EG.
- Chứng minh tứ giác HMKI là hình bình hành:
Ta có: H là trung điểm của GE (gt)
I là trung điểm của GB (gt)
=> HI là đường trung bình của (1)
+) Tứ giác ABKM là hình bình hành ( cm câu a)
Mà E đối xứng với B qua A => A là trung điểm của BE
(2)
Từ (1) và (2) => tứ giác HMKI là hình bình hành
- Suy ra GH = GK, GI = GM, từ đó ta có => G là trọng tâm tam giác DEF cũng là trọng tâm tam giác ABC.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
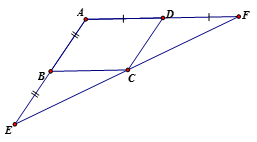
E là điểm đối xứng của A qua B (gt) nên AB = BE
Tứ giác ABCD là HBH =>
Mà AB = BE (cmt) => Tứ giác BDCE là hình bình hành
=> BD // EC và BD = EC.
Chứng minh tương tự cũng có BD // CF và BD = CF.
Vì BD // EC và BD // CF => E, C, F thẳng hàng (tiên đề Ơ-clit) Mà EC = CF (= BD) nên C là trung điểm EF => E là điểm đối xứng của F qua C.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
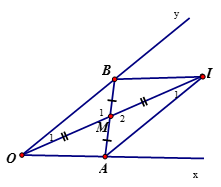
Cách dựng:
- Dựng điểm I đối xứng với O qua điểm M.
- Qua I dựng đường thẳng song song với Oy cắt Ox ở A.
- Dựng đường thẳng AM cắt Oy ở B.
Chứng minh:
Xét và có:
( hai góc so le trong)
MO = MI ( Vì I và O đối xứng nhau qua M)
( hai góc đối đỉnh)
=> (g.c.g) => MA = MB ( 2 cạnh tương ứng)
Bài toán luôn luôn dựng được một và có một nghiệm hình.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập