Câu hỏi:

19/08/2025 1,641

Một người đo chiều cao của một cây nhờ chôn một cọc xuống đất, cọc cao 2m và đặt xa cây 15m. Sau khi người lùi xa cách cọc 0,8m thì nhìn thấy đầu cọc và đỉnh cây cùng nằm trên một đường thẳng. Hỏi cây cao bao nhiêu mét, biết rằng khoảng cách từ chân đến mắt người ấy là 1,6m?

Xem lời giải

Câu hỏi trong đề: Bài tập Toán 8 Chủ đề 10: Ứng dụng thực tế của tam giác đồng dạng có đáp án !!

Giao bài

Quảng cáo

Trả lời:

Giải bởi Vietjack

Học sinh tự vẽ hình

Minh họa đề bài bằng vẽ hình, ta có:

Chiều cao của cây là $A A^{'}$ .
Độ dài của cọc là $B B^{'} = 2 m$ .
Khoảng cách từ chân đến mắt người đo là $M N = 1, 6 m$ .
Khoảng cách từ cọc đến cây là $A^{'} B^{'} = 15 m$ .
Khoảng cách từ người đo đến cọc là $N B^{'} = 0, 8 m$ .

Từ M kẻ $M K$ vuông góc với AA' thì cũng vuông góc với BB' tại H (vì $B B^{'} // A A^{'}$ ).

Suy ra: $M K = M H + H K = N B^{'} + A^{'} B^{'} = 0, 8 + 15 = 15, 8 (m)$

$B H = B B^{'} - H B^{'} = B B^{'} - M N = 2 - 1, 6 = 0, 4 (m)$

Xét $Δ M H B ∽ Δ M K A$ (hai tam giác vuông có chung góc M)

$\Rightarrow \frac{B H}{A K} = \frac{M H}{M K} \Rightarrow A K = \frac{B H . M K}{M H} = \frac{0, 4.15, 8}{0, 8} = 7, 9 (m)$

Do đó, $A A^{'} = A K + K A^{'} = 7, 9 + 1, 6 = 9, 5 (m)$

Vậy, chiều cao của cây đo được là 9,5 mét.

Đang tải chế độ Học...

Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay

Các sản phẩm khác của Vietjack:

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Hình 58 mô tả dụng cụ đo bề dày của một số loại sản phẩm. Dụng cụ này gồm thước AC được chia đến 1mm và gắn với một bản kim loại hình tam giác ABD, khoảng cách $B C = 10 mm$ .

Muốn đo bề dày của vật, ta kẹp vật vào giữa bản kim loại và thước (đáy vật áp vào bề mặt của thước AC). Khi đó trên thước AC ta đọc được “bề dày” d của vật (trên hình vẽ ta có: $d = 5, 5 cm$ ).

Hãy chỉ rõ định lý nào của hình học là cơ sở để ghi các vạch trên thước $A C (d \leq 10 mm)$ .

Xem đáp án

Lời giải

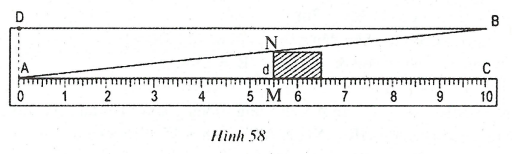
Ta có $M N // B C \Rightarrow Δ A M N ∽ Δ A C B$

$\Rightarrow \frac{A M}{A C} = \frac{M N}{B C} \Rightarrow M N = \frac{A M . B C}{A C} = \frac{A M .10}{100} = \frac{1}{10} A M$ .

Do đó, khi đọc $A M = 5, 5 cm$ thì đọc $M N = d = \frac{1}{10} .5, 5 cm = 5, 5 mm$ .

Trong bài toán này, ta đã áp dụng định lí: “Nếu một đường thẳng cắt hai cạnh của một tam giác và song song với cạnh còn lại thì tạo thành một tam giác mới đồng dạng với tam giác đã cho” để ghi lại các vạch trên thước AC.

Câu 2

Để đo khoảng cách từ hai địa điểm A và B, trong đó B không tới được, người ta tiến hành đo và tính khoảng cách AB như hình 57 với $A B // D F; A D = m; D C = n; D F = a$ .
Tính độ dài x của khoảng cách AB.

Xem đáp án

Lời giải

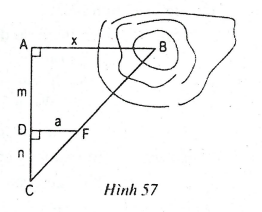
Media VietJack

Ta đo độ dài m, n và a rồi tính độ dài x như sau:

Do $D F // A B$ (cùng vuông góc với AC)

$\Rightarrow Δ C D F ∽ Δ C A B \Rightarrow \frac{C D}{C A} = \frac{D F}{A B} \Rightarrow A B = \frac{C A . D F}{C D} = \frac{(m + n) a}{n}$

Vây, ta được $x = \frac{(m + n) a}{n}$ .

Câu 3

Để đo khoảng cách từ hai địa điểm A và B, trong đó B không tới được, người ta tiến hành đo và tính khoảng cách AB như hình 57 với $A B // D F; A D = m; D C = n; D F = a$ .

Em hãy nói rõ cách đo như thế nào?

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Xem thêm các câu hỏi khác »

Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.

Lớp 12

Lớp 11

Lớp 10

Ôn vào 10

Lớp 9

Lớp 8

Lớp 7

Lớp 6

Ôn vào 6

Lớp 5

Lớp 4

Lớp 3

Lớp 2

Lớp 1

Đại học

ĐGNL - ĐGTD

Tốt nghiệp THPT

Ôn vào 10

Ôn vào 6

V-ACT

HSA

TSA

SPT

Toán

Văn

Tiếng Anh

Vật lý

Hóa học

Sinh học

Lịch sử

Địa lý

Giáo dục Kinh tế và Pháp luật

Tin học

Công nghệ

Toán

Văn

Tiếng Anh

Vật lí

Hóa học

Sinh học

Lịch sử

Địa lí

Giáo dục Kinh tế và Pháp luật

Tin học

Công nghệ

Toán

Văn

Tiếng Anh

Vật lí

Hóa học

Sinh học

Lịch sử

Địa lí

Giáo dục Kinh tế và Pháp luật

Tin học

Công nghệ

Toán

Văn

Tiếng Anh

Vật lý

Hóa học

Sinh học

Lịch sử

Địa lí

Giáo dục Kinh tế và Pháp luật

Tin học

Công nghệ

Toán

Văn

Tiếng Anh

Vật lý

Hóa học

Sinh học

Khoa học tự nhiên

Tin học

Lịch sử

Địa lí

Toán

Văn

Tiếng Anh

Để đo khoảng cách từ hai địa điểm A và B, trong đó B không tới được, người ta tiến hành đo và tính khoảng cách AB như hình 57 với $A B // D F; A D = m; D C = n; D F = a$ .
Tính độ dài x của khoảng cách AB.

Để đo khoảng cách từ hai địa điểm A và B, trong đó B không tới được, người ta tiến hành đo và tính khoảng cách AB như hình 57 với $A B // D F; A D = m; D C = n; D F = a$ .

Em hãy nói rõ cách đo như thế nào?