Câu hỏi:

19/08/2025 1,105

Cho hình thang ABCD có $A B = a, C D = b$ . Qua giao điểm O của hai đường chéo, kẻ đường thẳng song song với AB, cắt AD và BC theo thứ tự ở E và G. Chứng minh rằng $\frac{1}{O E} = \frac{1}{O G} = \frac{1}{a} + \frac{1}{b}$ .

Câu hỏi trong đề: Bài tập Toán 8 Chủ đề 1 và 2: Tổng hợp định lí ta-lét, tam giác đồng dạng và các bài toán liên quan có đáp án !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

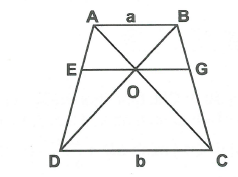
Media VietJack

Vì $O E / / A B$ nên $\frac{O E}{A B} = \frac{D E}{D A} \Leftrightarrow \frac{O E}{a} = \frac{D E}{D A}$ (theo hệ quả định lý Ta-lét) (1).

Vì $O E / / C D$ nên $\frac{O E}{D C} = \frac{A E}{D A} \Leftrightarrow \frac{O E}{b} = \frac{A E}{D A}$ (theo hệ quả định lý Ta-lét) (2).

Từ (1) và (2) ta được

$\frac{O E}{a} + \frac{O E}{b} = \frac{D E}{D A} + \frac{A E}{D A} = 1 \Leftrightarrow O E (\frac{1}{a} + \frac{1}{b}) = 1 \Leftrightarrow \frac{1}{a} + \frac{1}{b} = \frac{1}{O E}$

Tương tự có: $\frac{1}{a} + \frac{1}{b} = \frac{1}{O G}$

Vậy $\frac{1}{O E} = \frac{1}{O G} = \frac{1}{a} + \frac{1}{b}$ .

Hot: 1000+ Đề thi giữa kì 1 file word cấu trúc mới 2025 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Một đường thẳng đi qua đỉnh A của hình bình hành ABCD cắt BD, BC, DC theo thứ tự ở E, K, G. Chứng minh rằng: $\frac{1}{A E} = \frac{1}{A K} + \frac{1}{A G}$

Xem đáp án

Lời giải

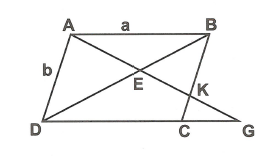
Media VietJack

Vì $A D / / B K \Rightarrow \frac{A E}{A K} = \frac{D E}{D B} A B / / D G \Rightarrow \frac{A E}{A G} = \frac{B E}{B D}$ ;

nên $\frac{A E}{A K} + \frac{A E}{A G} = \frac{D E}{B D} + \frac{B E}{B D} = \frac{B D}{B D} = 1 \Rightarrow \frac{1}{A K} + \frac{1}{A G} = \frac{1}{A E}$

Vậy $\frac{1}{A K} + \frac{1}{A G} = \frac{1}{A E}$ .

Câu 2

Một đường thẳng đi qua đỉnh A của hình bình hành ABCD cắt BD, BC, DC theo thứ tự ở E, K, G. Chứng minh rằng: Khi đường thẳng thay đổi vị trí nhưng vẫn đi qua A thì tích BK.DG có giá trị không thay đổi.

Xem đáp án

Lời giải

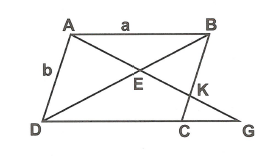
Media VietJack

Đặt $A B = a, A D = b$

Vì $A B / / C G \Rightarrow \frac{B K}{K C} = \frac{A B}{C G} = \frac{a}{C G}; A D / / C K \Rightarrow \frac{K C}{A D} = \frac{C G}{D G} = \frac{K C}{b}$ ; nên $\frac{B K}{a} = \frac{b}{D G}$

$\Rightarrow B K . D G = a . b$ (hằng số).

Vậy khi đường thẳng thay đổi vị trí nhưng vẫn đi qua A thì tích BK.DG có giá trị không thay đổi.

Câu 3

Một đường thẳng đi qua đỉnh A của hình bình hành ABCD cắt BD, BC, DC theo thứ tự ở E, K, G. Chứng minh rằng: $A E^{2} = E K . E G$

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 4

Cho hình thang ABCD ( $A B / / C D$ ). Điểm E thuộc cạnh AD, điểm F thuộc cạnh BC sao cho $\frac{D E}{D A} = \frac{B F}{B C} = \frac{1}{3}$ . Gọi M, N theo thứ tự là giao điểm của EF với BD, AC.

Chứng minh rằng EM=NF.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Xem thêm các câu hỏi khác »

Toán

Văn

Vật lý

Hóa học

Lịch sử

Địa lý

Sinh học

Công nghệ

Tin học

Tiếng Anh

Giáo dục Kinh tế và Pháp luật

ĐHQG Hồ Chí Minh

ĐH Bách Khoa

ĐHQG Hà Nội

Bộ Công an

ĐHSP Hà Nội

Bằng lái xe

English Test

IT Test

Đại học

Toán

Văn

Vật lý

Hóa học

Lịch sử

Địa lý

Sinh học

Công nghệ

Tin học

Giáo dục Kinh tế và Pháp luật

Toán

Văn

Vật lý

Hóa học

Lịch sử

Địa lý

Sinh học

Công nghệ

Tin học

Giáo dục Kinh tế và Pháp luật

Toán

Văn

Vật lý

Hóa học

Lịch sử

Địa lý

Sinh học

Tin học

Giáo dục Kinh tế và Pháp luật

Global success

iLearn Smart World

Friends Global

Explore new worlds

Toán

Văn

Vật lý

Hóa học

Lịch sử

Địa lý

Sinh học

Công nghệ

Tin học

Giáo dục Quốc Phòng và An Ninh

Giáo dục Kinh tế và Pháp luật

Toán

Văn

Vật lý

Hóa học

Lịch sử

Địa lý

Sinh học

Công nghệ

Tin học

Giáo dục Quốc Phòng và An Ninh

Giáo dục Kinh tế và Pháp luật

Toán

Văn

Vật lý

Hóa học

Lịch sử